Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.1 - Ex. 22
Trace a curva e estime visualmente seu comprimento. A seguir, encontre seu comprimento exato.
Passo 1
Primeiro a gente estima visualmente:
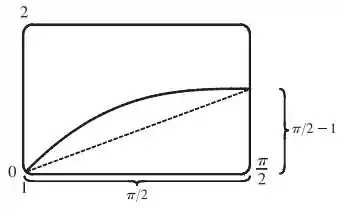
Passo 2
Pela figura, o comprimento da curva é suavemente mais largo que a hipotenusa do triângulo formado pelos pontos , , e . Esse comprimento é mais ou menos , então nós devemos estimar o comprimento para ser .
Passo 3
Então,
Resposta
.
Exercícios de Livros Relacionados
22. A densidade linear em um ponto de uma barra de 5 m varia diretamente com a distância do ponto a um ponto externo à barra sobre a sua reta suporte e a 2 m de um extremo, onde a densidade é K kg/m.
25. Uma barra L cm de comprimento e o centro de massa da barra está num ponto a 3 4 L do extremo esquerdo. Se a medida da densidade linear num ponto for proporcional a uma potência da medida da distân
22- Comprimento de um astroide O gráfico da equação x 2 / 3 + y 2 / 3 = 1 faz parte de uma família de curvas chamadas astroides (e não asteroides) por causa de sua aparência de estrela (veja a figura
Nos Exercícios 1-10, determine o comprimento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são.8- y = x 3 3 + x 2 + x + 1 4 x + 4 ,0 ≤ x ≤
27- Existe uma curva lisa y = f ( x ) (continuamente derivável) cujo comprimento ao longo do intervalo 0 ≤ x ≤ a seja sempre 2 a ? Justifique sua resposta.