Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.2 - Ex. 43
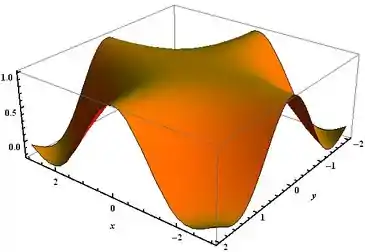
Trace o gráfico e analise a continuidade da função
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos traçar o seu gráfico e verificar a continuidade na função.
Para isso, iremos utilizar uma ferramenta gráfica para a plotagem e iremos comparar a continuidade da função com a figura.
Agora bora lá!! 😉
Passo 2
Show de bola, galera! Agora vamos dar uma olhada no gráfico da nossa função para observar o seu comportamento.
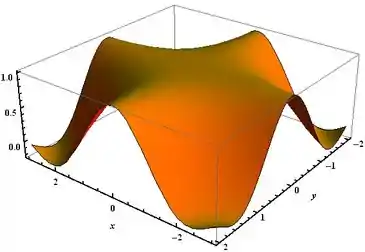
Como podemos observar do gráfico, a nossa função é contínua para todo o .
Se pensarmos em pegar qualquer ponto tal que e definirmos uma função , calcularemos o seguinte limite:
Esse é um limite fundamental que o seu resultado é:
Dessa forma, percebemos que a nossa função é realmente contínua para todo o .
Perceba também que o resultado bate com o gráfico no ponto , onde a função é igual a .
Resposta
