Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 7e

Transformar a seguinte equação para coordenadas polares.

x 2 + y 2 - 2 x = 0

Passo 1

As coordenadas polares r ,   θ   podem ser transformadas em coordenadas cartesianas ( x , y ) pela seguinte substituição:

x = r cos ⁡ θ

y = r sin ⁡ θ

Esses resultados podem ser concluídos pela definição de seno e cosseno. Observe a figura abaixo:

cos ⁡ θ = x r ⇒ x = r cos ⁡ θ

sin ⁡ θ = y r ⇒ y = r sin ⁡ θ

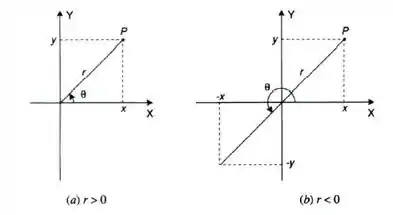
De forma análoga, as coordenadas cartesianas podem ser transformadas em coordenadas polares. Elevando ambos os membros das equações a cima ao quadrado, podemos escrever:

x 2 = r 2 cos 2 ⁡ θ

y 2 = r 2 sin 2 ⁡ θ

Adicionando membro a membro, obtemos:

x 2 + y 2 = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ ⇒ x 2 + y 2 = r 2

Assim, podemos reescrever nossa função da seguinte forma:

x 2 + y 2 - 2 x = 0 ⇒ r 2 - 2 r cos ⁡ θ = 0 ⇒ r - 2 cos ⁡ θ = 0 ⇒ r = 2 cos ⁡ θ

Resposta

r = 2 cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a área da região limitada por um laço da curva r = as e nn θ , onde n é um número inteiro positivo.
Ache a equação polar da circunferência com centro em ( r 0 ,θ 0 ) e raio a unidades.
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço do gráfico. A reta rs e n θ = 6 é a diretriz correspondente ao foco na origem e e = 5 3 .
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço do gráfico. Um foco na origem; Um vertice em ( 6 ,1 2 π ); e = 1 ;
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço do gráfico. Um foco na origem; um vértice em (6, 1 2 π ); e = 3 4 .