Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.16 - Ex. 12

Usar o teorema da divergência para calcular a integral da superfície dada.

∬ S x 2 d y d z + y 2 d z d x + z 2 d x d y

Sendo S a superfície exterior do tetraedro delimitado pelos planos coordenados e pelo plano x + y + z = 1

Passo 1

O teorema da divergência relaciona uma integral tripla sobre um sólido e uma integral dupla sobre a superfície fronteira deste sólido.

Seja T um sólido no espaço, limitado por uma superfície orientável S . Se n → é a normal unitária exterior a S e se f → = f 1 i → + f 2 j → + f 3 k → é uma função vetorial contínua que possui derivadas parciais de 1 ª ordem contínuas em um domínio que contém T , então

∬ S f → ⋅ n → d S = ∭ T ∇ ⋅ f → d V

Assim tendo introduzido formalmente o nosso teorema, podemos agora começar a aplica-lo e começar a nos familiarizarmos com ele.

Passo 2

A Primeira coisa que vamos fazer, é tentar identificar algumas coisas que nos foram dadas

Temos que nossa f → é

f → = ( x 2 , y 2 , z 2 )

E assim temos que o divergente será

∇ ⋅ f → = ( ∂ x 2 ∂ x + ∂ y 2 ∂ y + ∂ z 2 ∂ z = 2 x + 2 y + 2 z

Depois temos que identificar o nosso sólido. A função que descreve nosso plano é

z = 1 - x - y

Onde no plano x y , ou seja, z = 0 temos que a projeção do nosso é um triangulo com seus limites definidos em x ∈ 0,1 e y ∈ 0,1 - x . Como a ideia é define os limites de integração a fim de descrever nosso volume, temos que seguir a seguinte estratégia

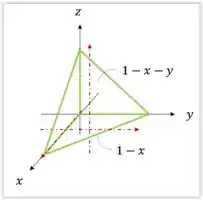
Vamos definir nossos limites de integração como sendo

0 ≤ x ≤ 1

0 ≤ y ≤ 1 - x

0 ≤ z ≤ 1 - x - y

Passo 3

Assim nossa integral será

2 ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x - y x + y + z d z d y d x

Que é uma integral simples, mas bastante trabalhosa

2 ∫ 0 1 ∫ 0 1 - x x z + y z + z 2 2 0 1 - x - y d y d x

Que fica

= 2 ∫ 0 1 ∫ 0 1 - x - x 2 2 - y 2 2 - x y + 1 2 d y   d x

Seguindo integrando agora em y , temos

= ∫ 0 1 - x 2 y - y 3 3 - 2 x y + x 2 0 1 - x d x

Que fica

= ∫ 0 1 x 3 3 - x + 2 3 d x = 1 12 - 1 2 + 2 3 = 1 4  

Resposta

1 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Suponha que S e C satisfaçam as hipóteses do Teorema de Stokes, e feg tenham derivadas parciais de segunda ordem contínuas. Use os exercícios 24e26 da seção 16.5 para demonstrar o seguinte: ∫ C f ∇ g
Calcule ∫ C y + s e n x d x + z 2 + c o s y d y + x 3 d z Onde C é a curva r → t = s e n t ,c o s t ,2 t , 0 ≤ t ≤ 2 π . (Sugestão: observe que C está na superfície z = 2 x y )
Use o Teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S → . F → x , y , z = 2 yc o s zi → + e xs e n zj → + x e y k → , S é o hemisfério x 2 + y 2 + z 2 = 9 ,z ≥ 0 , orientado para cima.
Seja C uma curva fechada simples lisa que está no plano x + y + z = 1 . Mostre que a integral de linha ∫ C z d x - 2 x d y + 3 y d z depende apenas da área da região englobada por C e não da forma de