Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.5 - Ex. 50
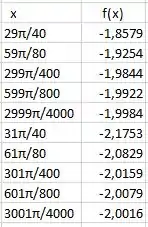
- Use uma calculadora para tabular até quatro casas decimais os valores de quando x é , , , , e x é , , , , . A que quociente parece tender quando x se aproxima de ?
- Ache , interpretando-o como uma derivada.
Passo 1
A letra a) nos pede para calcular o valor da função dada no enunciado para cada um dos valores de x, depois devemos aproximar o resultado em até quatro casas decimais, ou seja, faremos um arredondamento dos resultados, e depois colocaremos em uma tabela:
Passo 2
Com o primeiro valor que deram para a gente , vamos substituir na função f(x):
Agora já podemos calcular o valor das cossecantes e das frações no denominador:
Resolvendo as subtrações e a divisão:
Passo 3
Agora podemos arredondar o valor da função f para quatro casas decimais:
Passo 4
Podemos repetir os mesmos passos para cada valor de x dado no enunciado, e com eles vamos montar a tabela abaixo:
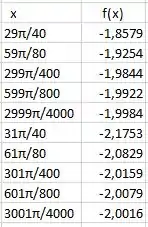
Os cinco primeiros valores de x se aproximam de e os valores da função se aproximam para por valores menores, enquanto os cinco últimos se aproximam por valores maiores, na medida que x se aproxima de .
Passo 5
Já na letra b) a questão pede para calcularmos o limite dado, mas através de uma interpretação de derivada.
Com isso, pegamos a definição de derivada:
E comparamos com o limite que foi dado:
Podemos perceber que o limite é a derivada da função cotangente no ponto , então fazendo a derivada:
E substituindo na nossa derivada:
