Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.10 - Ex. 55
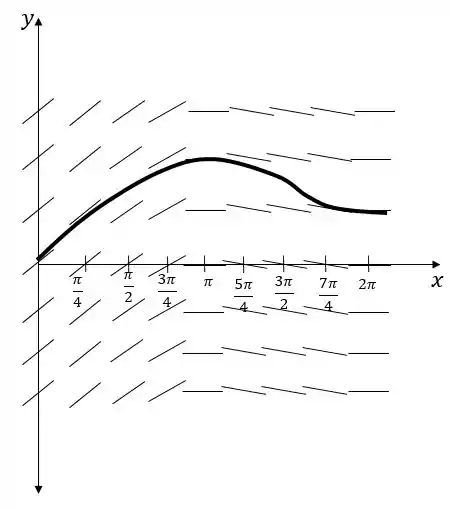
Use um campo de direção para fazer o gráfico da antiderivada que satisfaça .
Passo 1
Pessoal, nessa questão devemos usar um campo de direções para traçar a antiderivada da função
Com entre
O campo de direções é feito calculando o valor da função para alguns valores de e então fazendo pequenos segmentos de reta com uma inclinação igual a , todos eles feitos na reta vertical .
Por exemplo, para , a função não existe, mas temos , então na reta vertical fazemos vários pequenos segmentos de inclinação 1 (45°, pois 1 é a tangente de 45).
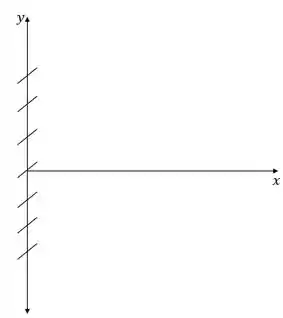
Como nos foi dado que deve respeitar , então temos que a deve passar na origem. Dessa forma, escolheremos o segmento de reta que passa na origem no desenho acima.
Passo 2
Vamos então calcular a função para alguns valores de 0 a :
Para
Para
Para
Para
(Opa vemos aqui que na reta , teremos segmentos de reta horizontais).
Para
Para
Para
Para
Assim conseguimos esboçar nosso campo de direções:
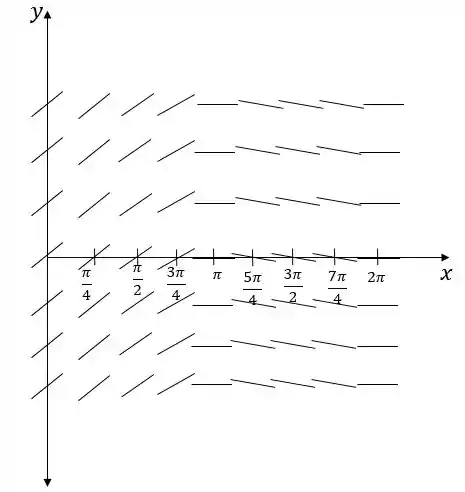
Passo 3
Agora usamos o campo de direções para traçar . Começamos a partir de , e então seguimos as direções dadas pelo campo. O gráfico então fica assim:
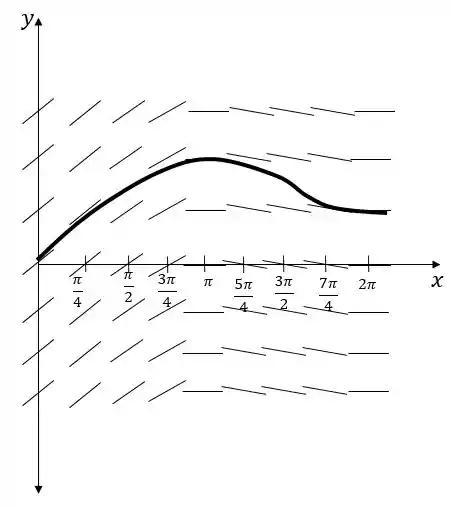
Resposta
