Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 79
Use um computador para investigar a família de superfícies . Em particular, você deve determinar os valores de transição para os quais a superfície muda de um tipo de superfície quádrica para outro.
Passo 1
Eaee, belezinha?? Bom... queremos utilizar um software matemático para plotar várias funções no seguinte formato:
Onde é uma constante.
Aqui a gente vai aplicar alguns valores de e ir plotando. Com isso, iremos analisar o que acontece quando alteramos o valor de , certinho??
Agora bora lá!! 😉
Passo 2
Vamos analisar os gráficos para alguns valores de .
Para :
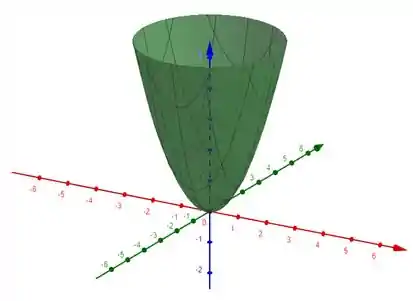
Passo 3
Agora vamos analisar alguns valores positivos de .
Para :
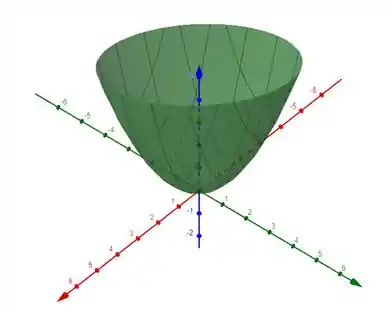
Para :
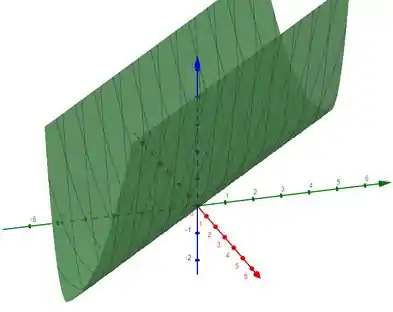
Para :
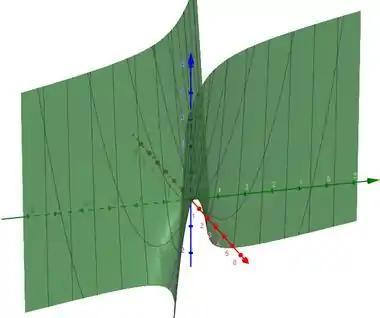
Passo 4
Agora vamos analisar alguns valores negativos de .
Para :
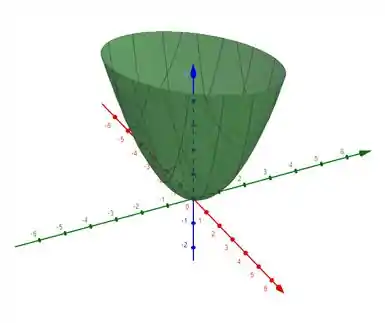
Para :
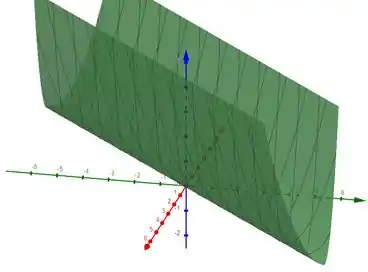
Para :
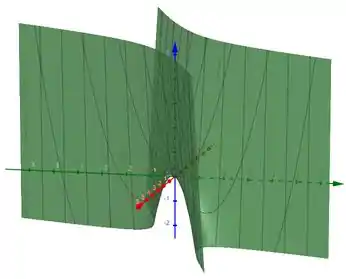
Passo 5
Podemos ver que o comportamento muda de maneira similar para valores de positivos e negativos, porém em uma reta diferente.
De maneira geral para temos um paraboloide padrão da forma , mas achatada, dependendo do valor de .
Para temos uma elipse esticada, da maneira como uma função com uma das variáveis ao quadrado e a outra constante (ex: , superfície), mas rotacionado em uma direção dependendo do sinal de .
Para temos uma função que se comporta como um paraboloide padrão em uma direção e como um paraboloide negativo na direção perpendicular. Essas direções dependem do sinal de .
Pela analise, podemos dizer que o ponto de transição é .