Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 62
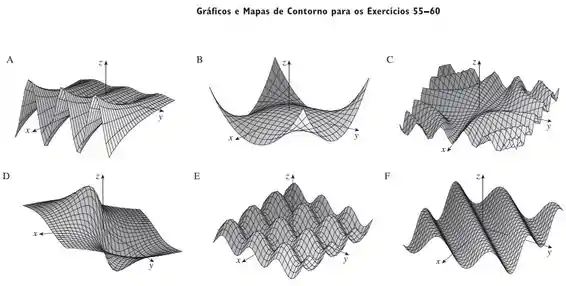
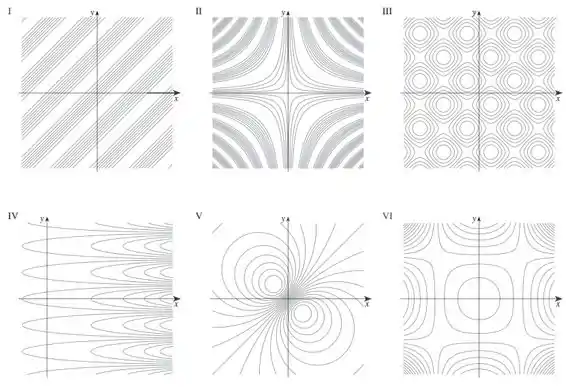
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha.
Passo 1
Falaaa, meu parceiro. É o seguinte, vamos resolver essa atividade juntos e você vai sair daqui sabendo tudo.
Temos então a função:
E queremos relacionar qual o gráfico dessa função e qual sua curva de nível, dentre as várias opções que nos foram dadas.
Para escolhermos corretamente qual o gráfico tridimensional dessa função, deveremos analisar o comportamento da mesma em determinados pontos, isso nos dará algumas dicas.
Vamos analisar aqui também o comportamento da nossa função quando e , isso irá nos ajudar a ver o que acontece nos planos e .
Passo 2
(a) a função , em relação à variável vai de no limite com e aumenta em toda a sua variação, já em relação a a função oscila entre positivo e negativo.
Quando , ou seja, os pontos onde a curva encontra o plano , temos , que é uma curva exponencial.
Quando , ou seja, os pontos onde a curva encontra o plano , temos , que é uma curva sinusoidal.
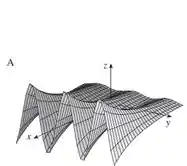
O gráfico que representa esse comportamento é o A.
Passo 3
(b) Para um fixo, o gráfico é apenas o de , para algum que depende de . , ou seja, ele aumenta exponencialmente conforme aumenta.
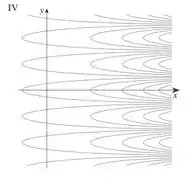
A partir disso, pode-se ver que A é o gráfico correto da função. Projetando os conjuntos de nível do gráfico A, obtemos a seção transversal .
Resposta
- A
- IV