1. Use a fórmula para mostrar que a área da superfície gerada pela rotação da curva polar

(Onde é contínua e ) em torno do eixo polar é

2. Use a fórmula na parte para calcular a área da superfície gerada pela rotação da lemniscata

Em torno do eixo polar.

Derivando e em relação a , usando a regra do produto:

Elevando ao quadrado:

Agora substituindo os termos e na fórmula da área, temos:

Isolando e

E considerando a relação trigonométrica , obtemos

Bingo! Encontramos a equação da área da superfície gerada em

Pensou que tínhamos acabado? Agora vamos usar a fórmula pra calcular a área de uma superfície real!

Nossa superfície é gerada pela rotação da curva

Aplicando a seguinte equação do Geogebra obtemos a curva.

Gráfico:

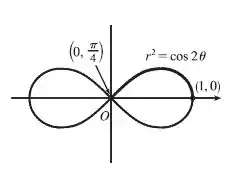
Queremos a área da superfície gerada quando essa curva gira em torno do eixo polar, gráfico mostrado anteriormente.

Se você reparar, a curva cruza a origem quando intersecta a ela mesma, assim

Assim, para obter a área da superfície, vamos girar o pedaço da curva que vai de até e depois multiplicar isso por 2. Com isso teremos a área da superfície inteira gerada pela rotação da curva, beleza?

Bora lá então.

Derivando implicitamente em relação a :

Elevando isso ao quadrado:

Substituindo na integral os valores de

Obtemos e seguinte equação

Realizando o MMC no interior da raiz quadrada, temos a relação trigonométrica . Sendo assim

Simplificando os termos semelhantes, a integral resulta na seguinte função.

Chegou a hora de resolvermos a integral.

Essa é a área de apenas metade da figura, pois nosso limite de integração foi de a Multiplicando por teremos a área total da suprficie.