Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 32

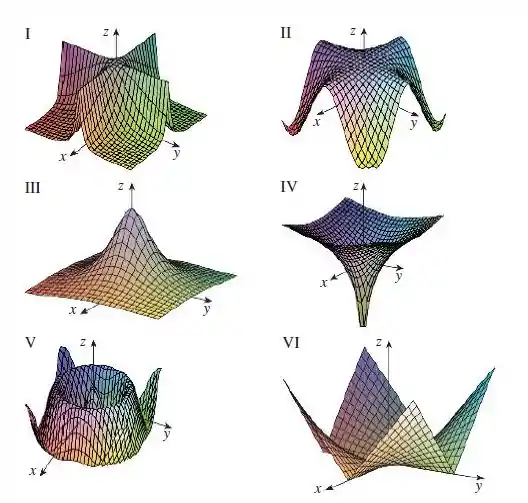
Combine a função com seu gráfico (rotulado I-VI). Dê razões para suas escolhas.

  1. f x , y = 1 1 + x 2 + y 2
  2. f x , y = 1 1 + x 2 y 2
  3. f x , y = ln ⁡ x 2 + y 2
  4. f x , y = cos ⁡ x 2 + y 2
  5. f x , y = x y
  6. f x , y = cos ⁡ ( x y )

Passo 1

Para relacionarmos a função com o gráfico podemos analisar a projeção de cada coordenada. Para fazer isso façamos y = 0 para o plano x z e x = 0 para o plano y z .

Passo 2

a) A função é f x , y = 1 1 + x 2 + y 2 = z

Quando x = 0 , temos:

z = 1 1 + y 2

Quando y = 0 , temos:

z = 1 1 + x 2

Desta forma quando quando x = 0   e   y = 0 temo que z = 1

Então o gráfico que corresponde a esta função tem um comportamento parecido com um paraboloide elíptico com concavidade para baixo. Logo o gráfico é o III (3).

Passo 3

b) A função é f x , y = 1 1 + x 2 y 2 = z

Quando x = 0 e y = 0 temos que z = 1 , isso significa que o gráfico está começando no ponto ( 0,0 , 1 ) .

Se fazermos x = y teremos:

1 1 + x 4 = z

Ou

1 1 + y 4 = z

O que nos diz que z decresce no formato de uma função elevada a x 4 , ou seja, um formato parabólico que decai muito mais rápido. Portanto o griafico que contém essa análise é o II (2).

Passo 4

c) A função é f x , y = l n ⁡ ( x 2 + y 2 ) = z

Quando x = 0 , temos:

z = ln ⁡ x ² = 2 ln ⁡ x

Quando y = 0 , temos:

z = ln ⁡ y ² = 2 ln ⁡ y

Como temos uma função l n ,então quando z   tende a 0 , x e y também tende a 0 , logo temos duas assíntotas. Pontanto o gráfico é o IV (4)

Passo 5

d) ) A função é f x , y = cos ⁡ x 2 + y ² = z

Quando x = 0 , temos:

z = cos ⁡ y 2 = cos ⁡ y

Quando y = 0 , temos:

z = cos ⁡ x 2 = cos ⁡ x

Logo o gráfico precisa ter a forma de um cosseno ao longo dos eixos x e y (picos e vales crescendo ao longo de uma circunferência), desta forma o gráfico que contém esse resultado é o V (5).

Passo 6

e) A função é f x , y = x y = z

Quando x = 0 e y = 0 temos que z = 0 , isso significa que o gráfico está começando no ponto ( 0,0 , 0 ) . Já z irá crescer com o módulo do plano x y .

Portanto o gráfico que representa está função é o VI (6).

Passo 7

f) A função é f x , y = cos ⁡ x y = z

Quando x = 0 e y = 0 temos que z = 1 , isso significa que o gráfico está começando no ponto ( 0,0 , 1 ) . Se fizermo x = y teremos:

z = cos ⁡ x 2

Ou

z = cos ⁡ y ²

Desta forma o gráfico que se relaciona com estas análises é o I (1).

Resposta

a) III

b) II

c) IV

d) V

e) VI

f) I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico das funções f x , y = x 2 + y 2 f x , y = e x 2 + y 2 f x , y = ln ⁡ x 2 + y 2 f x , y = sen ⁡ x 2 + y 2 f x , y = 1 x 2 + y 2 Em geral, se g é uma função de uma variável, como obter
64. Descreva as superfícies de nível da funçãof (x , y , z) = x^2 - y^2
66. Descreva como o gráfico de g é obtido a partir do gráfico de f a) g x , y = f ( x - 2 ,y ) b) g x , y = f ( x ,y + 2 ) c) g x , y = f ( x + 3 ,y - 4 )