Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 25

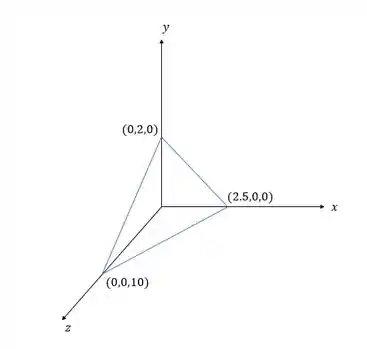
Esboce o gráfico da função.

Passo 1

E aí, pessoal. Beleza?

Aqui nessa questão nós temos a fun��ão e queremos esboçar o seu gráfico. Para fazer isso, vamos primeiro entender um pouco mais sobre essa função e depois fazer o seu gráfico.

Vamos olhar pra nossa função:

Que é a mesma coisa que:

Rearrumando, com todas as variáveis pro mesmo lado:

Trata-se da equação de um plano.

Agora vamos ver no próximo passo, como fazemos o gráfico de um plano.

Passo 2

Sabemos que três pontos definem um plano. Então, basta encontrarmos quais quer três pontos que satisfaçam a equação

e teremos o plano dado por essa equação.

A forma mais simples de obter esses pontos consiste em deixar duas variáveis como zero e descobrir o valor da terceira variável para satisfazer a equação acima.

Vamos lá...

Fazendo obtemos:

Fazendo , otemos:

Por último, fazendo , otemos:

Portanto, os pontos e satisfazem a equação do plano.

Passo 3

Agora que sabemos três pontos desse plano, podemos representar esse gráfico como:

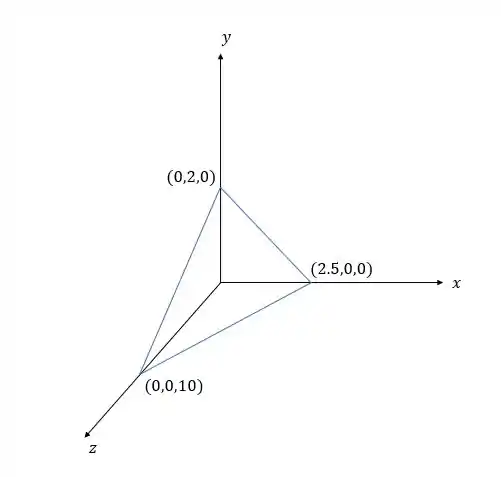
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ponto P descreve uma curva sobre a superíıcie z=x y de modo que a sua proje¸c˜ao Q sobre o plano xy descreve a curva x = 5 - t , y= t ²+3ez= 0 ² . Determine as alturas máxima e mínima (em relação a

Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = I R ² ²

Desenhe as curvas de nível e esboce o gráfico da função. f x , y = x + 1 2 + y ² + x - 1 2 + y ² ² ²

Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A, bem como os pontos em que estes valores são atingidos. f x , y = x + yeA = x , y ∈ I R 2x ≥ 0 , y ≥ 0, x +

Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = x , y ∈ I R 2 4 x 2 + y 2 = 1 ,y ≥ 0 }