Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 69

Use a geometria ou simetria, ou ambas, para calcular a integral dupla.

∬ D a x 3 + b y 3 + a 2 - x 2 d A ,       D = - a , a × - b , b

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Este tipo de questão é interessante pois nos cobra o uso de propriedades (quando falamos de simetria estamos pensando na paridade de funções) ou na comparação do sólido com o volume de uma figura.

Vamos começar por entender a nossa região D . Como ela é uma região retangular simétrica em alguma função impar dentro da nossa integral, o seu resultado será 0 .

Analisando as funções f x = a x 3 e g y = b y 3 , percebemos que elas são funções ímpares!! Logo, o resultado final da sua integração será 0 .

Sabendo disso, a integral da nossa questão pode ser reescrita por:

∬ D a x 3 + b y 3 + a 2 - x 2 d A = ∬ D a 2 - x 2 d A

Passo 2

Para podermos resolver a questão, precisamos identificar que sólido é este que estamos trabalhando, para assim relacionar a integral com o seu volume. Se fizermos z = a 2 - x 2 , obtemos uma superfície cilíndrica!!

Este cilindro pode ser visualizado:

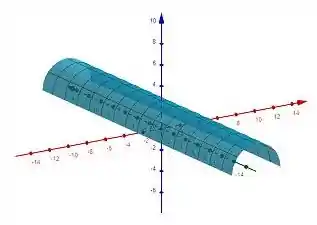
Portanto, o volume dele será dado pela área da base (que está no planp x z ) pela altura, que está ao longo do eixo y . Portanto:

V = A b a s e ⋅ A l t u r a

V = π a 2 2 ⋅ 2 b = π a 2 b

Desta forma, temos:

∬ D a x 3 + b y 3 + a 2 - x 2 d A = π a 2 b

Resposta

∬ D a x 3 + b y 3 + a 2 - x 2 d A = π a 2 b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dupla.∬_R^() (6 x^2 y^3 - 5 y^4) d A , R = {(x , y)| 0 = x = 3 , 0 = y = 1 }
Calcule a integral dupla. ∬ Rx 1 + x yd A, R = 0 ,1 × 0 ,1
Calcule a integral dupla. ∬ R1 + x 2 1 + y 2 d A R = x ,y0 ≤ x ≤ 1,0 ≤ y ≤ 1 }
Calcule a integral dupla. ∬ Rx y 2 x 2 + 1 d A R = x ,y0 ≤ x ≤ 1,- 3 ≤ y ≤ 3 }
Calcule a integral dupla.∬_R^() cos ( x + 2 y ) d A , R = {(x , y)| 0 = x = pi , 0 = y = pi // 2 }