Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.2 - Ex. 18

Calcule a integral dupla.

∬ R   1 + x 2 1 + y 2 d A                    

R = x ,   y   0 ≤ x ≤ 1   ,   0 ≤ y ≤ 1 }  

Passo 1

E ai pessoal, tudo bem?

Vamos entender o enunciado juntos!? Ele nos forneceu uma integral dupla com limites de integração na região R e precisamos determinar o valor dessa integral.

∬ R   1 + x 2 1 + y 2 d A                    

R = x ,   y   0 ≤ x ≤ 1   ,   0 ≤ y ≤ 1 }  

Vish, agora lascou? Calma, vamos pensar juntos!

Primeiro é importante lembrar, que sempre começamos a integrar de dentro para fora. Assim vamos montar a nossa integral, de forma que começamos a integrar por d y . Mas deve tomar cuidado, pois precisamos fazer uma substituição trigonométrica e ir fazendo as manipulações para resolver.

Você deve chamar:

y = tan ⁡ θ

d y = sec 2 ⁡ θ   d θ

Sabendo disso, a integral deve ficar com essa carinha de início:

∫ 0 1 ∫ 0 1 1 + x 2 1 + y 2   d y d x

Observe que os limites de integração a gente tira da região R , ele forneceu isso no enunciado:

0 ≤ x ≤ 1

0 ≤ y ≤ 1

Agora você vai debulhar a questão, vamos começar a integrar!? Partiu então!

Passo 2

Vamos começar relembrando nossa integral, já com os limites fornecido na região R :

∫ 0 1 ∫ 0 1 1 + x 2 1 + y 2   d y d x

Nossa primeira etapa, vai ser integrar em d y , logo tudo que não depende de y será uma constante.

Assim, podemos reescrever:

∫ 0 1 ( 1 + x 2 ) ∫ 0 1 1 1 + y 2   d y d x

Agora é a hora que precisamos fazer uma substituição trigonométrica:

y = tan ⁡ θ

d y = sec 2 ⁡ θ   d θ

Aplicando na integral, temos:

∫ 0 1 ( 1 + x 2 ) ∫ 0 1 1 1 + ( tan ⁡ θ ) 2 sec 2 ⁡ θ   d θ d x

∫ 0 1 ( 1 + x 2 ) ∫ 0 1 sec 2 ⁡ θ   1 + tan 2 ⁡ θ d θ d x

Sabendo da relação trigonométrica,

1 + tan 2 ⁡ θ = sec 2 ⁡ θ  

Temos,

∫ 0 1 ( 1 + x 2 ) ∫ 0 1 1 d θ d x

Logo, nossa integral fica

∫ 0 1 ( 1 + x 2 ) θ 0 1 d x

Passo 3

Muito cuidado nessa hora de aplicar os limites de integração, pois esses limites são para y e não para θ .

Logo, vamos substituir θ por y novamente para mantermos os limites de integração.

y = tan ⁡ θ

Fazendo o inverso, temos

θ = arctan ⁡ y

Agora sim,

∫ 0 1 ( 1 + x 2 ) arctan ⁡ y 0 1 d x

Aplicando os limites,

∫ 0 1 ( 1 + x 2 ) arctan ⁡ 1 - arctan ⁡ 0 d x

Vamos analisar graficamente a função arctan ⁡ y .

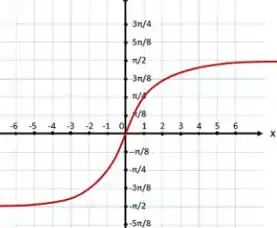
Avaliando o gráfico, concluímos que

arctan ⁡ 1 = π 4

arctan ⁡ 0 = 0

Logo,

∫ 0 1 ( 1 + x 2 ) π 4 d x

Passo 4

Agora, basta resolver cada integral simples em d x .

∫ 0 1 ( 1 + x 2 ) π 4 d x

Integrando, temos que:

π 4 x + x 3 3 0 1

Aplicando os limites de integração:

π 4 1 + 1 3 3

Logo, o resultado da integral é:

∫ 0 1 ∫ 0 1 1 + x 2 1 + y 2   d y d x = π 3

Resposta

π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dupla.15. ∬ D y 3 d A D é a região triangular com vértices 0,2 ,( 1,1 ) e ( 3,2 ) .
Calcule a integral dupla. ∬ D( x + y ) d A, Dél i m i t a d ap o ry = x,y = x 2 é
Determine o volume do sólido dado.25.Abaixo da superfície z = x y e acima do triângulo com vértices ( 1,1 ) , ( 4,1 ) e ( 1,2 )
Calcule a integral dupla. ∬ D 2 x - y d A D é limitada pelo círculo de centro na origem e raio 2
Calcule a integral dupla. ∬ D 2 x yd A D é a região triangular com vértices 0 , 0 ,( 1 , 2 ) e ( 0 , 3 ) .