Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 27

Calcule a integral, efetuando uma mudança de variáveis apropriada.

∫ ∫ R e x + y   d A , onde R é dada pela inequação

x + y ≤ 1

Passo 1

Pessoal, vamos usar a seguinte transformação:

u = x + y   ,     v = - x + y

Assim, se olhássemos essas equações como um sistema e o resolvesse, encontraríamos:

x = 1 2 ( u - v )   ,     y = 1 2 ( u + v )

E então podemos calcular o jacobiano da transformação:

∂ ( x ,   y ) ∂ ( u ,   v ) = 1 2 - 1 2 1 2 1 2 = 1 2

Passo 2

Agora observe o que acontece quando usamos a desigualdade triangular (propriedade do módulo) e a inequação do enunciado:

u = x + y ≤ x + y ≤ 1

Ou seja,

u ≤ 1 ⇒ - 1 ≤ u ≤ 1

Analogamente, para v :

v = - x + y ≤ x + y ≤ 1

v ≤ 1 ⇒ - 1 ≤ v ≤ 1

Isso significa que acabamos de encontrar os novos limites de integração. Também poderíamos conseguir isso observando um esboço de R :

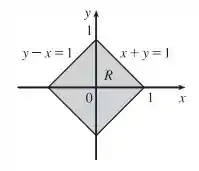
Passo 3

Beleza! Juntando todas as informações que obtivemos até aqui, somos capazes de escrever a nova integral e calculá-la:

∫ ∫ R e x + y   d A = ∫ - 1 1 ∫ - 1 1 e u 1 2   d u   d v = 1 2 ∫ - 1 1 e u d u ∫ - 1 1 d v = 1 2 e u - 1 1 v - 1 1 = 1 2 e - e - 1 2 = e - 1 e

Resposta

e - 1 e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a transformação φ de ℝ2 em ℝ2 dada por x = u + v e y = u − v. Desenhe φ (B)sendo B a reta v = 0. sendo B o quadrado 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
Calcule
Calcule
Calcule
Exercício de Livro