Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 64
Use um gráfico da sequência para decidir se ela é convergente ou divergente. Se a sequência for convergente, conjecture o valor do limite a partir do gráfico e então demonstre sua conjectura.
Passo 1
Fala galera! Tudo certo?
A questão já nos dá :
então precisamos plotar seu gráfico. Para isso usamos softwares como GeoGebra ou Excel e aí analisando a curva formada vamos poder entender se a sequência tende a algum valor específico ou não, ou seja, se é divergente ou convergente.
Antes de plotar vamos calcular alguns termos só para fins de esclarecimento de como obter os primeiros termos.
Vamos lá!
Passo 2
Show, vamos testar alguns pontos então pra poder entender a lógica:
Para , temos:
Para , temos:
Para , temos:
Para , temos:
Vamos deixar que o gráfico nos mostre os próximos termos:
Plotando o gráfico, temos:
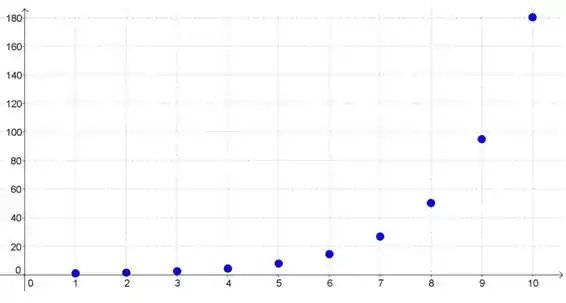
Parece que nossa sequência apenas cresce cada vez mais, tendendo a infinito. Então ela diverge, beleza?
Resposta
Sequência divergente