Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 4

Use o gráfico dado de para dizer o valor de cada quantidade, se ela existir. Se não existir, explique por quê .

(b) (c)

(d) (e) (f)

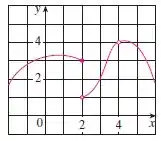
Passo 1

Eaee, belezinha?? Bom... o enunciado nos deu o seguinte gráfico de uma função :

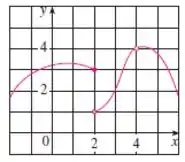
Queremos, a partir do gráfico, analisar os limites laterais, os limites e as funções da função:

Para resolvermos isso, temos que saber dos limites laterais.

Mas o que são esses limites??

Bom... Os limites laterais descrevem o comportamento de uma função em relação a um ponto específico, considerando abordagens à direita e à esquerda desse ponto.

Lembrando que o limite só existe em um ponto se os limites laterais forem iguais!!

Agora bora aplicar!! 😉

Passo 2

Vamos analisar primeiro esse limite:

Como , devemos começar a analisar o gráfico pela esquerda até chegarmos em :

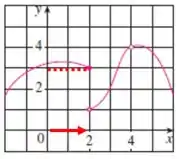
Assim, analisando desse modo, quando , se aproxima de, logo

Passo 3

Agora, vamos analisar esse outro limite:

Como , devemos começar a analisar o gráfico pela direita:

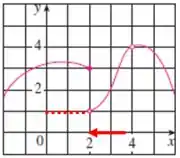
Assim, analisando desse modo, quando , se aproxima de, logo:

Passo 4

Agora vamos analisar esse limite:

Para , devemos considerar os limites pela esquerda e pela direita.

Pelo que vimos no passo 1, temos que o limite só existe em um ponto se seus limites laterais forem iguais, ou seja:

Logo, como os limites laterais (pela esquerda e pela direita) são diferentes, concluímos que não existe.

Passo 5

Para , devemos observar no gráfico qual o valor de quando :

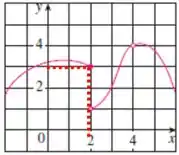
Assim, temos que .

Outra maneira de saber, em gráficos descontínuos como este, é verificar para aquele ponto de descontinuidade, neste caso em ,qual ponto tem uma “bolinha fechada”, isso indica que pertence a imagem.

Passo 6

Agora vamos analisar o limite .

Quando , analisando o gráfico, começando tanto pela esquerda quanto pela direita, temos que se aproxima de, veja:

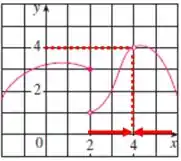
Logo, por definição, como os limites lateras são iguais, temos que:

Passo 7

Agora vamos verificar .

Apesar do limite existir quando , o gráfico é descontínuo neste ponto (verifica-se isso por possuir uma “bolinha aberta” neste ponto do gráfico, o que significa que não tem imagem naquele ponto).

Portanto, não existe.