Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.4 - Ex. 1
Use o gráfico dado de para encontrar um número tal que
se então
Passo 1
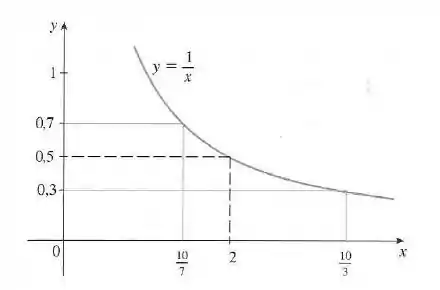
Opa, bora lá! Aqui temos o seguinte gráfico:
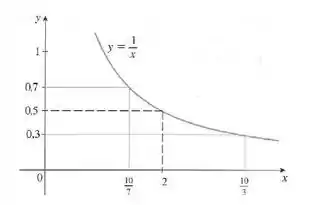
Nesta questão, a gente quer encontrar . Então primeiro vamos trabalhar com o intervalo que a questão deu e depois substituir na função.
O enunciado forneceu a seguinte desigualdade para acharmos o :
Tirando do módulo das seguintes formas:
e
Repara que uma é positiva e outra negativa. Vamos resolver as duas!
Começando pela positiva:
Agora vamos para segunda fórmula:
Assim temos:
Agora precisamos determinar os valores de para os quais a curva está entre as restas horizontais e .
Passo 2
Para achar os valores de , nós vamos interver o que achamos em para . Como:
Passando o para o numerador, invertando essa fração, temos
Vamos melhorar a cara desse intervalo,
Substituindo esses limites em . Vemos que esse intervalo não é simétrico em torno de , a distância até a extremidade esquerda será:
E a distância até a extremidade direita é
Assim vamos escolher como o menor desses números, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.