Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.4 - Ex. 55
Use um gráfico de para decidir se é positiva ou negativa. Utilize o gráfico para dar uma estimativa aproximada do valor da integral e então use as frações parciais para encontrar o valor exato.
Passo 1
Fazendo o esboço da curva, temos que
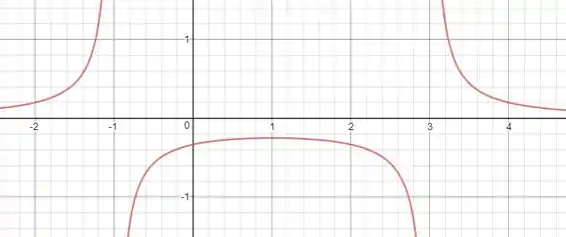
Como no intervalo até a função é negativa, a integral é negativa. Além disso, podemos estimar a integral por um retângulo de base e altura . Assim,
Passo 2
Agora vamos calcular a integral usando frações parciais e comparar com nossa estimativa. Primeiro vamos resolver a equação
Obtemos
Assim, . Desta forma,
Assim, e . Portanto, e . Logo,
Passo 3
Desta forma,
Fazendo essa conta em uma calculadora, obtemos
Note que é bem próximo de nossa estimativa!
Resposta
Exercícios de Livros Relacionados
43. Em qualquer instante, a taxa segundo a qual uma substância se dissolve é proporcional ao produto da quantidade presente em qualquer instante pela diferença entre a concentração da substância na so
35.Um dia em um campus universitário com 5.000 alunos, onde se esperava uma assembleia estudantil um aluno ouviu que certo estudande polêmico iria fazer, durante a assembleia, um discurso explosivo. E
Nos exercícios de 1 a 20, calcule a integral indefinida.15. ∫ x 2 + 2 x - 1 d x 27 x 3 - 1
Nos exercícios de 1 a 20, calcule a integral indefinida.11. ∫ 2 x 2 - x + 2 d x x 5 + 2 x 3 + x
Nos exercícios de 1 a 20, calcule a integral indefinida.18. ∫ ( 2 x 2 + 3 x + 2 ) d x x 3 + 4 x 2 + 6 x + 4