Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.3 - Ex. 38

Use um gráfico para encontrar as coordenadas aproximadas no eixo x dos pontos de intersecção das curvas y = x + ln ⁡ x e y = x 3 - x . Então, encontre (aproximadamente) o centroide da região limitada por essas curvas.

Passo 1

Bom galera, nesse exercício queremos encontrar o centroide da região delimitada pelas curvas. Para isso, iremos esboçar o gráfico gerado pelas funções e observar a região e seus pontos de interseção. Depois iremos utilizar as técnicas de integração e as definições de centroide para encontrar aproximadamente o local exato aonde se encontra o centroide.

Passo 2

Esboçando a curva, temos

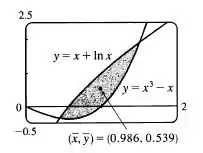
Podemos ver com base no gráfico que os pontos de interseção são aproximadamente

a ,   c = 0.447141 ,   - 0.357742

b ,   c = 1.507397 ,   1.917782

A área da região será então

A = ∫ a b x + ln ⁡ x - x 3 + x d x = ∫ a b 2 x + ln ⁡ x - x 3 d x

Resolvendo a integral, temos

A = x 2 + x ln ⁡ x - x - x 4 4 a b = 0.709781

Passo 3

Podemos então calcular o centroide da seguinte maneira

x - = 1 A ∫ a b x x + ln ⁡ x - x 3 + x d x = 1 0.709781 ∫ a b 2 x 2 + x ln ⁡ x - x 4 d x

x - = 1 0.709781 2 3 x 3 + x 2 4 2 ln ⁡ x - 1 - x - x 5 5 a b = 0.985501

y - = 1 A ∫ a b 1 2 x + ln ⁡ x 2 - x 3 - x 2 d x

y - = 1 2 A x 2 ln ⁡ x - x 2 2 + x ln ⁡ x 2 - 2 x ln ⁡ x + 2 x - x 7 7 + 2 x 5 5 a b = 0.538964

Resposta

x - ,   y - = 0.985501 ,   0.538964

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.17.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.26.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.22.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.23.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.12.