Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.2 - Ex. 1g
Calcule o volume do sólido obtido pela rotação, em torno do eixo , do conjunto de todos os pares (x,y), tais que :
Passo 1
Uma questão um pouco diferente, por não conter as inequações em função apenas de , então, inicialmente vamos colocar em função de :
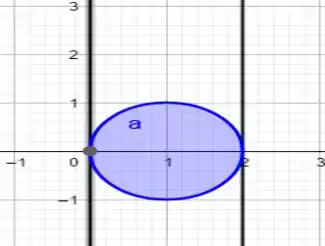
Região interna de uma circunferência de raio 1 e centro
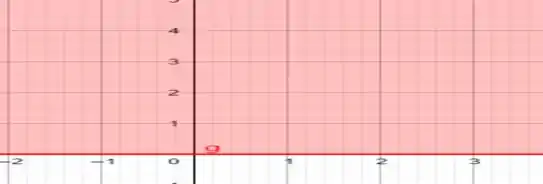
E agora da interseção entre esses dois gráficos, que está em verde, já com as retas que delimitam em preto.
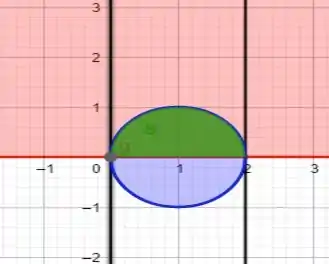
Passo 2
Nosso maior problema será a integração, então, anotaremos as informações para começarmos logo!
Intervalo de integração será de
Nossa função será
E a fórmula do volume é essa aqui ó:
Substituindo “dentro” da integral, teremos esse negócio aqui:
Essa integral não é imediata, iremos fazer uma mudança de variável:
Derivando para obtermos , teremos:
Agora colocando tudo que tem dentro da integral:
Passo 3
Focaremos nossa atenção na integral abaixo:
O método de resolução dela é por substituição trigonométrica, então vou botar o triângulo retângulo para auxiliar a gente, sem desespero, só precisamos ser organizados!
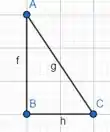
O cateto AB será dado pela função
O cateto BC será dado pela função
E a hipotenusa será dada pela função
Derivando, temos:
Substituindo tudo na integral da questão, temos:
Deixando essa integral mais amigável:
Calcularemos as integrais uma de cada vez
Chamaremos:
Derivando, temos:
Lembrando que:
Lembrando que:
Voltando a variável em u, temos isso aqui ó:
Voltando agora a variável em , não se embole, anote sempre as coisas, assim:
Colocando para dentro da integral, está acabando, vamos lá
Agora como último ato dessa questão, faremos a definida, uma vez que calculamos a indefinida acima: