Calcule o volume do sólido obtido pela rotação, em torno do eixo y , do conjunto de todos os pares (x,y), tais que : 1 ≤ x ≤ 4 1 ≤ y ≤ x

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.2 - Ex. 1f

Calcule o volume do sólido obtido pela rotação, em torno do eixo , do conjunto de todos os pares (x,y), tais que :

4

Passo 1

Percebemos que o não está delimitado pela função nula! Sempre que isso ocorrer, preste bastante atenção, pois teremos que fazer uma diferença de volumes para encontramos o volume que queremos!!!!

Sem mais enrolação, vamos começar pelo que nos dará a direção, dá uma olhadinha nesses gráficos que estão aqui embaixo:

Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:

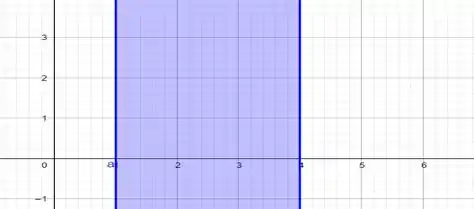
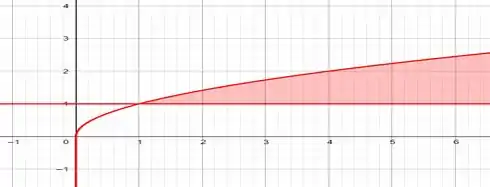
E agora da interseção entre esses dois gráficos, que está em verde:

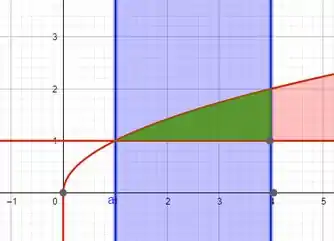
Passo 2

Como dito lá no início, iremos fazer uma subtração de volumes, mas quais serão essas que devemos utilizar?

Os limites de integração são:

E o volume que queremos será

Nossa querida fórmula!

Passo 3

Calcularemos :

Agora para darmos um fim a essa questão, faremos a subtração dos dois volumes e acharemos o que queremos!!!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y = s e nx ,y = cos ⁡

Encontre uma integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas sobre a reta especificada. Em seguida, use a calculadora para determinar a integral com precis

Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ - 1 1 ( 1 - y 2 )d y

Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região. y = 1 - x 2 ,y = 0 ; e mt o r n od oe i x ox