Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.1 - Ex. 55

Use um gráfico para encontrar as coordenadas aproximadas x dos pontos de intersecção das curvas dadas. A seguir, ache (aproximadamente) a área da região delimitada pelas curvas.

y = x   se n ⁡ x ,   y = ( x - 2 ) ²

Passo 1

O esboço do gráfico é o seguinte:

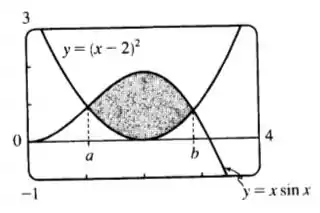
Passo 2

Nós encontramos a e b encontrando os pontos em que a função se interceptam, e isso acontece quando elas são iguais, então

x   se n ⁡ x = ( x - 2 ) ²

x   se n ⁡ x = x 2 - 4 x + 4

Resolvendo essa conta, temos que a ≈ 1.04748 e b ≈ 2.87307 .

Passo 3

Portanto, nossa área é

A = ∫ a b [ x   se n ⁡ x - ( x - 2 ) ² ] d x = - x   cos ⁡ x + se n ⁡ x - 1 3 x - 2 3 a b

Pelo Exemplo 1, temos que

A ≈ 2.81358 - 0.67074 = 2.18283

Resposta

A = 2.18283 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o centroide da região delimitada pelas curvas y = x 2 - x e y = x 2 - 1
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área até a quinta casa decimal. y = 2 1 + x 4 y = x 2
Calcule a integral.36. ∫ 0 1 1 + x 2 3 d x
Calcule a integral.37. ∫ 1 e x 2 + x + 1 xd x
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.16.