Use um gráfico para encontrar um número δ tal que x x 2 + 1 ⋅ x - 1 2100 sempre que 0x - 1δ .

Enunciado

Faaala galera,

Nessa questão precisamos plotar o gráfico da função

e ver em qual intervalo de valores de , a função é maior do que .

Com isso, olhando para esse intervalo, vamos ver quais são os valores de em que

Plotando o gráfico vamos ter

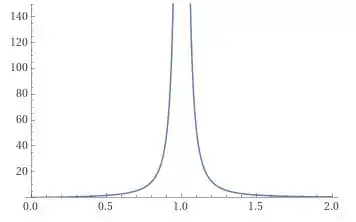
Para enxergar melhor o que está acontecendo, vamos dar um zoom nesse gráfico, usando uma janela gráfica melhor selecionada, estou usando aqui de e .

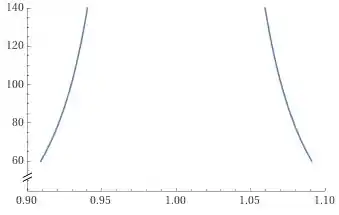
Pelo gráfico podemos perceber que nossa função é maior que sempre que se encontra no intervalo: .

Então vamos ter

Agora, vamos usar os valores limites do nosso intervalo de . Começando por .

E com , temos

Portanto, vemos que deve ser para que os valores de resultem em um .