Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.2 - Ex. 36

Use um gráfico para encontrar os valores aproximados das coordenadas x   dos pontos de intersecção das curvas dadas. A seguir, encontre (aproximadamente) o volume do sólido obtido pela rotação em torno do eixo x da região limitada por essas curvas.

y = 3 se n ⁡ ( x 2 ) ,   y = e x 2 + e - 2 x  

Passo 1

O gráfico formado é o seguinte:

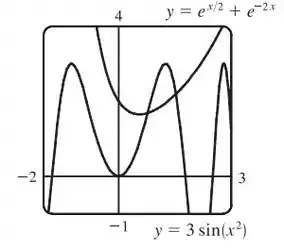
Passo 2

A duas funções se interceptam nos pontos x = a ≈ 0.772 e x = b ≈ 1.524 , informações tiradas do gráfico.

Passo 3

Calculamos o volume da seguinte maneira:

V = π ∫ a b { [ 3 se n ⁡ ( x 2 ) ] ² - ( e x 2 + e - 2 x ) ² } d x = π ∫ 0.772   1.524 { [ 3 se n ⁡ ( x 2 ) ] ² - ( e x 2 + e - 2 x ) ² } d x

V ≈ 7.519

Resposta

V ≈ 7.519

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume obtido pela rotação da região delimitada pelas curvas dadas em torno dos eixos especificados y = sin ⁡ x , y = cos ⁡ x , 0 ≤ x ≤ π 4 , e mt o r n od ey = 1
Encontre o volume obtido pela rotação da região delimitada pelas curvas dadas em torno dos eixos especificados y = sec ⁡ x , y = cos ⁡ x , 0 ≤ x ≤ π 3 , e mt o r n od ey = - 1
Encontre o volume obtido pela rotação da região delimitada pelas curvas dadas em torno dos eixos especificados y = sin 2 ⁡ ( x ) , y = 0 , 0 ≤ x ≤ π , e mt o r n od ee i x ox
Encontre o volume obtido pela rotação da região delimitada pelas curvas dadas em torno dos eixos especificados y = sin ⁡ x , y = 0 , π 2 ≤ x ≤ π , e mt o r n od oe i x ox
Encontre o volume comum de duas esferas, cada qual com raio r , se o centro de cada esfera está na superfície da outra esfera.