Use o gráfico da equação na figura abaixo para encontrar os sinais de e nos pontos A, B e C.
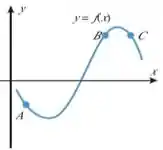
Passo 1
O enunciado nos pede pra encontrar os sinais das derivadas, primeira e segunda. Só olhando o gráfico, como sugerido, já é possível a gente encontrar os sinais e dar a reposta ao exercício.
A derivada primeira, , sempre tem sinal positivo em pontos em que, da esquerda pra direita, a função esteja crescendo. De maneira oposta, ela vai ter sinal negativo quando a função estiver decrescendo.
Já a derivada segunda, , vai ter sinal positivo quando o ponto estiver em uma região em que a função tiver concavidade voltada pra cima. Logo, terá sinal negativo quando a concavidade estiver voltada pra baixo.
Passo 2
Avaliando os pontos A, B e C no gráfico, podemos responder que:
A tem negativa e positiva
B tem positiva e negativa
C tem negativa e negativa.
Resposta
A tem negativa e positiva
B tem positiva e negativa
C tem negativa e negativa.