Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 12
Use o gráfico de para estimar o valor de
correto até a segunda casa decimal.
Use a tabela de valores de para estimar o limite até quatro casas decimais.
Passo 1
Bom galera, nesse exercício iremos estimar o valor do limite da função no infinito por dois métodos: O gráfico da função e uma tabela de valores de . Mas antes de qualquer coisa, vamos analisar a função pra poder escolher melhor os pontos:
O está no denominar e como expoente. Pensando no denominador, à medida que assume valores positivos maiores, então tende a zero. Mas tem o na frente, isso significa que será sempre positivo e menor ou igual a , desde que seja positivo.
Lembrando que, não precisamos pensar em valores de negativos, uma vez que o enunciado pede o limite para tendendo a infinito.
Dessa forma podemos pegar valores maiores que , uma vez que:
Passo 2
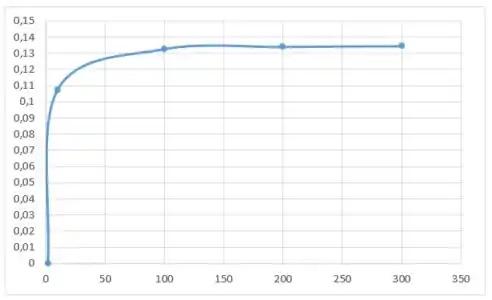
Utilizando o gráfico da função, estimamos que
Passo 3
Agora, fazendo uma tabela de valores para estimar o valor do limite, temos:
Pela tabela, estimamos que
Resposta
a)
b)