Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.4 - Ex. 63
Use um gráfico para estimar o valor do limite. Então use a Regra de L’Hospital para encontrar o valor exato.
Passo 1
Oieee, vamos lá,
Para estimar o valor do limite, usando um gráfico, precisamos traçar a função
Vou criar o gráfico para visualizarmos o comportamento da função conforme tende ao infinito.
Vamos usa regra de L’Hospital para encontrar o valor exato
Para encontrar o valor exato do limite usando a Regra de L'Hospital, começamos simplificando a expressão
Simplificamos o argumento do logaritmo:
Portanto, o limite se torna:
Passo 2
Aplicação da Regra de L'Hospital
A expressão
Ainda está na forma indeterminada .
Podemos reescrevê-la para aplicar a Regra de L'Hospital. Consideramos:
Agora, aplicamos a Regra de L'Hospital, diferenciando o numerador e o denominador:
Passo 3
Aplicando a Regra de L'Hospital, temos:
Quando a expressão se aproxima de
Portanto, o valor exato do limite é:
Passo 4
Agora vamos gerar o gráfico para confirmar nossa estimativa.
Codigo Matlab
% Definindo a função
f = @(x) x .* (log(x + 5) - log(x));
% Valores de x
x_values = linspace(1, 100, 400);
y_values = f(x_values);
% Criando o gráfico
figure;
plot(x_values, y_values, 'b', 'LineWidth', 1.5);
hold on;
% Adicionando uma linha horizontal em y = 5
plot(x_values, repmat(5, size(x_values)), 'r--', 'LineWidth', 1.5);
xlabel('x');
ylabel('f(x)');
title('Gráfico de x[ln(x+5) - ln(x)]');
legend('x[ln(x+5) - ln(x)]', 'y=5', 'Location', 'southeast');
grid on;
hold off;
Passo 5
Execução do código para visualização
Vamos executar o código acima para gerar o gráfico.
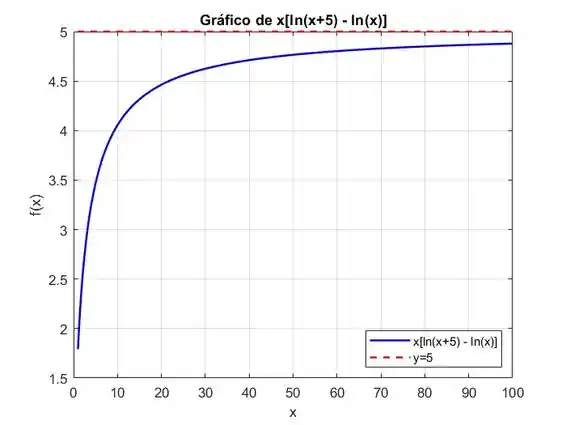
Conclusão do Gráfico
Ao observar o gráfico, podemos ver que conforme aumenta, a função se aproxima de , confirmando nossa solução analítica.
Portanto, o limite
é de fato