Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.4 - Ex. 64
Use um gráfico para estimar o valor do limite. Então use a Regra de L’Hospital para encontrar o valor exato.
Passo 1
Oie tudo bem galerinha, bora resolver mais uma juntinhos?
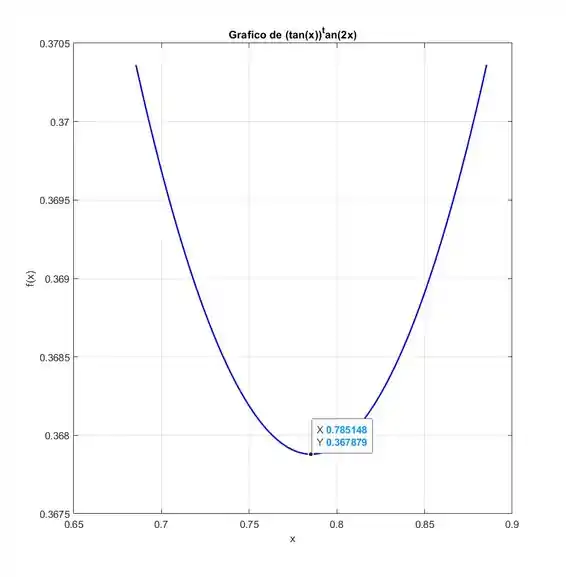
Para estimar o valor do limite
vamos traçar o gráfico da função para valores de próximos a .
Código MATLAB para gerar o gráfico
% Definindo a função
f = @(x) (tan(x)).^tan(2*x);
% Valores de x próximos a pi/4
x_values = linspace(pi/4 - 0.1, pi/4 + 0.1, 400);
y_values = f(x_values);
% Criando o gráfico
figure;
plot(x_values, y_values, 'b', 'LineWidth', 1.5);
xlabel('x');
ylabel('f(x)');
title('Grafico de (tan(x))^tan(2x)');
grid on;
Passo 2
Vamos usar a Regra de L’Hospital para encontrar o valor exato
Primeiro, reescrevemos a expressão em uma forma mais conveniente para aplicar a Regra de L'Hospital.
Vamos usar a transformação logarítmica:
Tomamos o logaritmo natural dos dois lados:
Então, o limite se transforma em:
Passo 3
Se encontrarmos este limite, podemos então encontrar o limite original ao aplicar a exponencial.
Análise do comportamento das funções
Quando :
-
- que tende a
Então, a expressão pode tender a uma forma indeterminada.
Vamos usar a Regra de L'Hospital para resolver isso.
Aplicação da Regra de L'Hospital
Reescrevemos o limite:
Passo 4
Derivamos numerador e denominador separadamente:
- Numerador:
- Denominador:
Aplicamos a Regra de L'Hospital:
Simplificando a expressão:
Passo 5
Substituímos na expressão:
Como
Passo 6
Sabemos que
Portanto:
Finalmente, voltamos à função original:
O valor exato do limite é .
O gráfico MATLAB deve mostrar que, conforme se aproxima de , a função tende a .