Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 66
(a) Use um gráfico para estimar os valores máximo e mínimo absolutos da função com precisão de duas casas decimais.
(b) Use o cálculo para encontrar os valores máximo e mínimo exatos.
Passo 1
E aí, tudo bom?! Nesse problema temos a seguinte função e o seu intervalo:
Aqui temos que achar os valores de máximo e mínimo de duas formas. Na primeira é uma estimativa, com precisão de duas casas decimais e pra isso vamos plotar o gráfico da função no intervalo dado!
Na segunda a gente vai encontrar esses valores através de cálculos! Para isso vamos, primeiro calcular a derivada de e iguala-la a zero para encontrar os números críticos. Depois a gente vai usar o método do intervalo fechado que é basicamente calcular nesses pontos e nos pontos extremos, e .
Vamos colocar a mão na massa!?
Passo 2
Vamos ver pelo gráfico primeiro...
Plotando, temos:
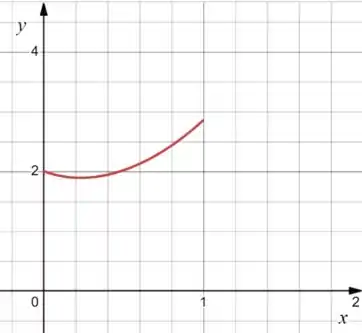
De cara vemos que o valor máximo fica no extremo , já o valor mínimo a gente vai precisar investigar passando o cursor do mouse pelo gráfico. Achamos então:
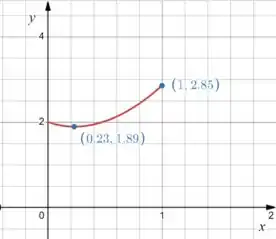
Então pelo gráfico nós vemos que o valor mínimo da função nesse intervalo é , localizado no ponto E o valor máximo, como já tínhamos visto, se encontra no ponto da extremidade , que resulta em .
Passo 3
Vamos para a letra b, onde precisamos derivar e igualar a derivada a zero:
Derivando:
Vamos ver quando isso vai ser zero...
Vamos reescrever pra tirar o negativo:
Aplicamos logaritmo dos dois lados:
Vamos testar então o valor da função nesse ponto e nos pontos do intervalo!
Passo 4
Agora vamos calcular nos pontos de interesse:
Vamos substituir e calcular:
Começando com :
Agora :
E finalmente:
Então, os valores máximos e mínimos exatos são:
Prontinhoo!
Resposta
- e .
- ;