Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 1
Use o gráfico de na figura abaixo para obter uma estimativa do valor de , , e .
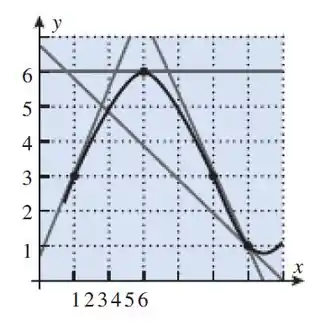
Passo 1
Para achar uma estimativa do valor de vamos achar a inclinação da reta tangente em .
Podemos achar a inclinação da forma:
Vamos então pegar dois pontos da reta em :
e
Agora é só substituir e pronto:
Agora vamos fazer o mesmo para os outros pontos.
Passo 2
Para achar uma estimativa do valor de vamos achar a inclinação da reta tangente em .
Aqui vemos que a reta tangente é paralela ao eixo , assim já sabemos que a inclinação nesse ponto é igual a zero.
Passo 3
Para achar uma estimativa do valor de vamos achar a inclinação da reta tangente em .
Podemos achar a inclinação da forma:
Vamos então pegar dois pontos da reta em :
e
Agora é só substituir e pronto:
Passo 4
Para achar uma estimativa do valor de vamos achar a inclinação da reta tangente em .
Podemos achar a inclinação da forma:
Vamos então pegar dois pontos da reta em :
e
Agora é só substituir e pronto: