Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 61
61.
(a) Use um gráfico de para estimar aproximadamente os intervalos da concavidade e as coordenadas dos pontos de inflexão.
(b) Use um gráfico de para uma estimativa melhor.
Passo 1
Fala aí, tudo certinho como você?
Bom, essa questão dá pra gente a função:
E pede pra gente responder a dois itens.
No item (a) teremos que usar o gráfico de para estimar aproximadamente os intervalos da concavidade e as coordenadas dos pontos de inflexão.
E para responder a esse item, precisamos saber que o ponto de inflexão em um gráfico é o lugar onde a função muda o sentido de sua concavidade.
No item (b) devemos usar um gráfico de para uma estimativa melhor.
E para isso devemos saber que se é negativa, então possui concavidade para baixo, se é positiva, então possui concavidade para cima e se é nula, temos um ponto de inflexão.
Agora que já sabemos o que fazer, bora resolver essa questão juntinhos.
Passo 2
Item a:
Pelo gráfico de :
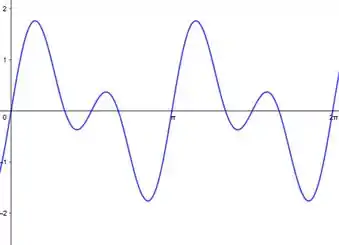
Passando para a escala de números inteiros, temos que
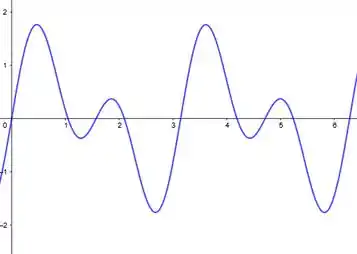
Então a concavidade é voltada para cima nos intervalos aproximados de:
E concavidade para baixo em
E seus pontos de inflexão são dados no momento de trocas de concavidade logo temos que
Passo 3
Show de bolinhas!!
Agora na letra (b), temos que analisar o gráfico de , isto é, da segunda derivada de . Primeiro vamos derivar ela e depois com a função vamos descobrir o gráfico.
Logo, o gráfico é:
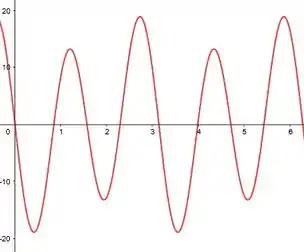
Se é negativa, então possui concavidade para baixo, se é positiva, então possui concavidade para cima e se é nula, temos um ponto de inflexão. Então a concavidade é voltada para cima nos intervalo aproximado de:
E concavidade para baixo em
E seus pontos de inflexão são:
Resposta
(a) A concavidade é voltada para cima nos intervalos aproximados de:
E concavidade para baixo em
E seus pontos de inflexão são:
(b) A concavidade é voltada para cima nos intervalo aproximado de:
E concavidade para baixo em
E seus pontos de inflexão são: