Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 14
Use o gráfico da função para dizer o valor de cada limite, se exisitir. Se não existir, explique por quê .
- (b) (c)
Passo 1
Eaee, belezinha??? Bom... o enunciado nos dá a seguinte função:
A partir dessa informação, devemos plotar o gráfico de e resolver os seguintes limites:
- (b) (c)
Aqui a gente vai trabalhar um pouco com os limites laterais.
Mas que limites são esses???
Bom... um limite lateral descreve o comportamento de uma função conforme nos aproximamos de um ponto a partir de diferentes direções no domínio da função.
Geralmente são divididos em limite lateral à esquerda (quando se aproxima pelos valores à esquerda de um número , ou seja, ) e limite lateral à direita (quando se aproxima pelos valores à direita de um número , ou seja, ).
Agora bora aplicar!! 😉
Passo 2
Primeiramente vamos plotar nosso gráfico:
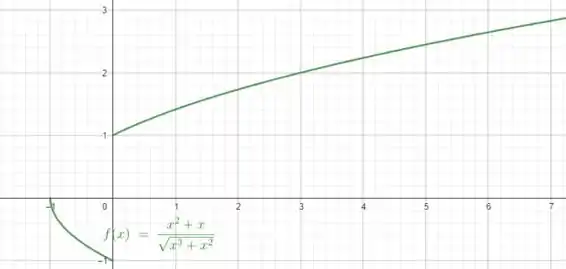
Agora vamos nos aproximar de zero olhando o gráfico para descobrir nossos limites!
Passo 3
Vamos fazer primeiro .
Se liga no que acontece quando fazemos se aproximar de pela esquerda ao selecionar pontos de :
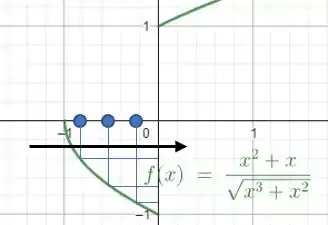
Perceba que quanto mais nos aproximamos de pela esquerda, tende a , logo:
Passo 4
Agora vamos fazer primeiro .
Se liga no que acontece quando fazemos se aproximar de pela direita ao selecionar pontos de :
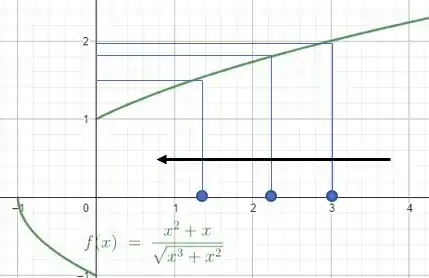
Perceba que quanto mais nos aproximamos de pela direita, tende a , logo:
Passo 5
Por fim, para achar , temos que verificar se os limites laterais são iguais.
Como os limites laterais são diferentes (observe os resultados obitdos em (a) e em (b)) e por definição temos que:
Se
E
Dessa forma, concluímos que não existe.
Resposta
- Não existe.