Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.1 - Ex. 59
Use um gráfico da sequência para decidir se ela é convergente ou divergente. Se a sequência for convergente, conjecture o valor do limite a partir do gráfico e então demonstre sua conjectura.
Passo 1
Fala Aí! Tudo certinho? Nessa questão precisamos decidir se a sequência é convergente ou divergente. Para isso, vamos precisar:
- Calcular os 5 primeiros termos da sequência.
- Traçar o gráfico da sequência.
- Verificar se a sequência tem um limite.
Vamos lá então?!
Passo 2
Primeiramente devemos descobrir quando vale os primeiros termos da sequência. Para descobrirmos isso, basta substituirmos por . Isso é bem tranquilo de fazer, não é mesmo? Sendo assim, teremos:
Para
Para
Para
Para
Para
Show?!
Passo 3
Agora vamos traçar o gráfico dessa sequência:
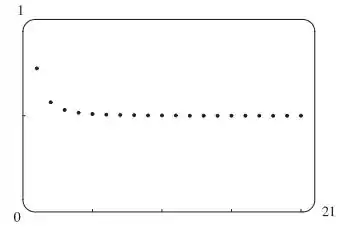
Ela com certeza é uma sequência convergente, pois depois de um tempo ela tende a um mesmo valor. E que valor será esse? Pelo gráfico, parece convergir pra , será que é isso mesmo?
Passo 4
Agora vamos calcular o limite da sequência pra confirmar nossa hipótese, tá ok?
Dividindo o numerador e o denominador pelo termo de maior grau , temos:
Fizemos essa divisão pela maior potência pra zerar termos e acabar com a indeterminação. Assim,
Realmente, nossa hipótese estava certa!
Resposta
Sequência convergente