Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 61

Use um gráfico da sequência para decidir se ela é convergente ou divergente. Se a sequência for convergente, conjecture o valor do limite a partir do gráfico e então demonstre sua conjectura.

a n = n 2 cos ⁡ n 1 + n 2

Passo 1

Galera, beleza? A questão quer que a gente use um gráfico da sequência para decidir se ela é convergente ou divergente. Depois, se a sequência for convergente, conjecturarmos o valor do limite a partir do gráfico e então demonstrarmos sua conjectura.

Vamos lá?! Antes de traçarmos o gráfico, vamos calcular alguns valores da sequência a n = n 2 cos ⁡ n 1 + n 2

para diferentes valores de   n .

Passo 2

Vamos calcular a n ​ para n = 1 ,   2 ,   3 ,   4   e   5 .

Para n = 1 :

a 1 = 1 2 cos ⁡ 1 1 + 1 2 = cos ⁡ 1 2 ≈ 0.877

Para n = 2 :

a 2 = 2 2 cos ⁡ 2 1 + 2 2 = 4 cos ⁡ 2 5 ≈ 0.554

Para n = 3 :

a 3 = 3 2 cos ⁡ 3 1 + 3 2 = 9 cos ⁡ 3 10 ≈ 0.087

Para n = 4 :

a 4 = 4 2 cos ⁡ 4 1 + 4 2 = 16 cos ⁡ 4 17 ≈ 0.015

Para n = 5 :

a 5 = 5 2 cos ⁡ 5 1 + 5 2 = 25 cos ⁡ 5 26 ≈ 0.000

Esses são alguns valores calculados da sequência para n = 1 ,   2 ,   3 ,   4   e   5 . Agora, podemos plotar esses pontos em um gráfico para observar o comportamento da sequência.

Passo 3

Agora vamos traçar o gráfico dessa sequência:

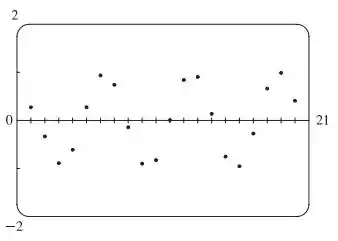
Parece que nossa sequência não converge pra nenhuma valor, né mesmo? Está sempre oscilando entre - 1   e 1 , por causa do cosseno. Então podemos concluir através do gráfico que a sequência diverge.

Resposta

Sequência divergente

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Convergência e divergência: Quais das sequências { a n } nos Exercícios 27-90 convergem? E quais divergem? Encontre o limite de cada sequência convergente.74. a n = ( 10 / 11 ) n ( 9 / 10 ) n+( 11 / 1
Convergência e divergência: Quais das sequências { a n } nos Exercícios 27-90 convergem? E quais divergem? Encontre o limite de cada sequência convergente.79. a n = n ⋅ s e n 1 n
Sequências definidas recursivamente: Nos Exercícios 91-98, assuma que cada sequência convirja e encontre o limite.91. a 1 = 2 ,a n + 1 = 72 1+a n
Teoria e exemplos: O primeiro termo de uma sequência é x 1 = 1 . Cada um dos termos seguintes é a soma de todos os seus antecedentes: x n + 1 = x 1+x 2+ ⋯ + x n . Escreva os primeiros termos da sequên
Convergência e divergência: Quais das sequências { a n } nos Exercícios 27-90 convergem? E quais divergem? Encontre o limite de cada sequência convergente.89. a n = 1 n ∫ 1 n 1 x d x