Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 60
Use um gráfico da sequência para decidir se ela é convergente ou divergente. Se a sequência for convergente, conjecture o valor do limite a partir do gráfico e então demonstre sua conjectura.
Passo 1
Pessoal, tudo certo por aí? Vem entender essa solução passo a passo:
A questão basicamente nos pede para traçar o gráfico da sequência e analisar através dele para que ponto nossa sequência vai convergir, caso haja a convergência.
Depois, para provar a convergência ou divergência da série, precisamos calcular o limite dela quando .
Para facilitar nossa análise, vamos usar propriedades da radiciação e da potenciação, que são operações presentes na nossa sequência, para simplificar nosso limite.
Passo 2
Galera, vamos primeiro traçar o gráfico dessa sequência (software: GeoGebra):
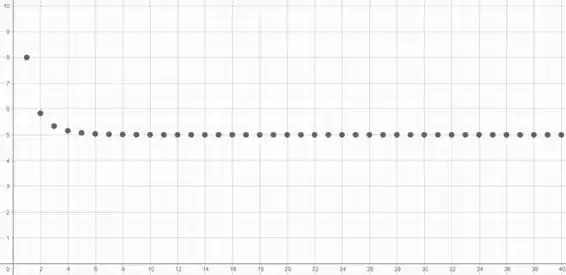
Aqui vemos que a sequência se aproxima cada vez mais de 5 quando vai crescendo. Nossa conjectura inicial é que o limite da nossa sequência existe e é 5.
Vamos conferir!
Passo 3
Vamos primeiro simplificar nosso limite. A estratégia que vamos tomar aqui é a tentar tirar termos de dentro da raiz e simplificar os que não podermos tirar. Então, vamos colocar em evidência:
Agora, nós podemos tirar o 5 para fora da raiz e rescrever nossa fração pela propriedade .
Reescrevendo novamente, temos:
Passo 4
Show! Agora vamos calcular o limite da sequência pra confirmar nossa hipótese, tá ok?
Assim, vemos que quando , nosso expoente tende a 0.
Como , teremos todo o termo que está multiplicando 5 igual a 1:
Realmente, nossa hipótese estava certa!
Resposta
Sequência convergente