Use um gráfico da sequência para decidir se ela é convergente ou divergente. Se a sequência for convergente, conjecture o valor do limite a partir do gráfico e então demonstre sua conjectura.

Antes de traçarmos o gráfico, Vamos calcular alguns valores da sequência

para diferentes valores de.

Vamos calcular ​ para .

Para :

Para :

Para :

Para :

Para :

Esses são alguns valores calculados da sequência para . Agora, podemos plotar esses pontos em um gráfico para observar o comportamento da sequência.

Ao traçar o gráfico dessa sequência, temos

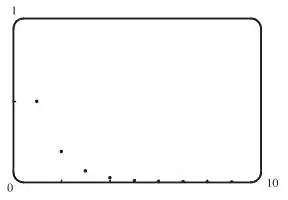
Parece que nossa sequência converge pra , né?

Pra confirmar nossa hipótese, vamos calcular o limite da sequência:

Mas como a gente resolve esse limite? Bom, vamos fazer tipo a regra do sanduíche à expressão

Primeiro, vamos observar que para todo .

Agora, vamos encontrar duas sequências, ​ e ​, tais que ​, e ambas convergem para o mesmo limite quando tende ao infinito.

Uma escolha natural para ​ é , já que ​ é sempre maior ou igual a zero. Para ​, podemos usar a expressão ​, que é uma sequência que sabemos que converge para zero porque os termos da sequência ficam arbitrariamente próximos de zero à medida que cresce.

Assim, teremos

Agora a gente toma o limite dessas expressões:

Sabemos que e .

Portanto, pelo Teorema do Sanduíche, a sequência ​ também converge para à medida que tende ao infinito. Então,

Como previmos!