Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 70
Use gráficos para estimar o valor do limite. A seguir, use a regra de L’Hospital para encontrar o valor exato.
Passo 1
Opa, bora resolver esse problema! Temos o limite:
E a primeira coisa que devemos fazer é estimar esse limite a partir de um gráfico. Aqui é muito simples, vamos plotar a função:
E localizar o ponto .
Depois disso precisamos calcular o limite na marra usando a regra de L’Hospital pra encontrar o valor exato! Essa regra diz que:
Só que só podemos usar essa regra quando temos uma indeterminação do tipo:
Então primeiro vamos substituir o valor de na função pra verificar se podemos usar essa regra de cara. Se a gente não encontrar essa indeterminação precisamos, primeiro, manipular a nossa função!
Vamos lá?!
Passo 2
Vamos começar esboçando o gráfico de :
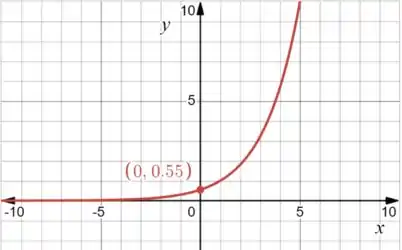
Vamos reter nossa atenção no entorno de . Note que a função se aproxima de .
Vamos usar isso como estimativa para o limite!
Passo 3
Nosso próximo objetivo é calcular o valor exato do limite:
Dessa forma, podemos aplicar a amada regra de L’Hospital!!!
Passo 4
Antes de aplicar a regra temos que lembrar da seguinte derivada:
Temos então que:
Calculando:
Podemos simplificar, lembrando da propriedade:
Então:
Vemos assim que nossa estimativa foi muito boa!!!