Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.2 - Ex. 2
Use os gráficos de e na figura a seguir para encontrar os limites que existirem. Se o limite não existir, explique por quê.
(a) (b)
(c) (d)
(e) (f)
(g) (h)
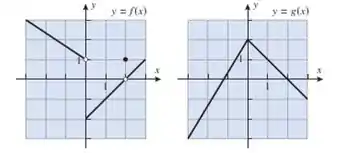
Passo 1
Aqui não tem dificuldade, apenas precisamos calcular os limites, considerando algumas das suas propriedades:
O limite de uma soma/subtração equivale à soma/subtração dos limites; o limite de um produto é o produto dos limites; o limite de um quociente é o quociente do limite – contanto que o limite não seja zero, etc.
Fora isso, agora temos o recurso dos gráficos pra nos ajudar no cálculo dos limites também! Por isso precisamos lembrar que, pra um limite existir, os limites laterais precisam existir e serem iguais, e valerem o mesmo que a função calculada no ponto!
Assim, já somos capazes de calcular todos esses limites!
Passo 2
(a)
O limite para não existe pois a função é descontínua em .
Passo 3
(b)
Passo 4
(c)
Passo 5
(d)
Passo 6
(e)
O limite para não existe pois a função é descontínua em .
Passo 7
(f)
O limite para não existe pois a função é descontínua em .
Passo 8
(g)
Passo 9
(h)
Resposta
(a) (b)
(c) (d)
(e) (f)
(g) (h)