Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.6 - Ex. 20
Use a integral tripla para determinar o volume do sólido dado.
O sólido delimitado pelo cilindro elíptico e pelos planos e
Passo 1
Oi, galera! Como estão?
A questão aqui pede que a gente calcule o volume do sólido delimitado pelo cilindro elíptico
e pelos planos
e
Para calcular o volume de um sólido, precisamos calcular a integral:
Onde é a região de integração do sólido no plano e
Então, o que falta para calcularmos nossa integral tripla são os limites de integração para cada uma das variáveis, e isso a gente consegue entendendo a descrição da região que o enunciado nos deu.
Com isso em mãos, é só a gente calcular a integral tripla de forma iterada, onde começamos pela “de dentro”, até chegarmos na última integral de fora. Assim, vamos ter o volume do sólido que procuramos.
Passo 2
Vamos encontrar os limites de integração. Plotando a descrição dos planos (verde) e
(azul) e do cilindro elíptico
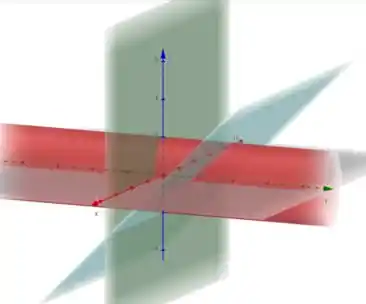
Como o próprio enunciado diz, nossa região está limitada entre dois planos em função de :
e
Então, podemos colocar a variação de como sendo
Para achamos o intervalo em , podemos isolar na equação do cilindro:
Isolando, teremos:
Aplicando a raiz quadrada na equação:
Podemos escrever a variação de como
Já que metade do cilindro está na parte positiva do eixo e a outra metade na parte negativa, como vemos na imagem.
Os intervalos de acontecem nos valores em que que são os valores máximo e mínimo de , já que a elipse está centrada na origem, então
Então
Passo 3
Pronto, agora temos nossos limites de integração e já podemos partir pro nosso cálculo. Nota que a gente coloca “pra dentro” as integrais com variáveis nos limites de integração, para facilitar nosso cálculo.
Calculando a integral, começando pela integral em , tratamos as demais variáveis como constantes. O resultado depois de aplicar os limites de integração é:
Integrando agora em :
Aplicando os limites de integração:
Simplificando:
Passo 4
Ufa! Calma que ainda falta nossa última integral em função de :
Vamos esquecer por enquanto os limites de integração e vamos fazer a substituição trigonométrica na integral
Substituindo
Derivando:
Substituindo:
Como:
Podemos substituir:
Usando:
Podemos substituir e finalmente resolver nossa integral:
Passo 5
Agora, vamos voltar para as variáveis que tínhamos antes da substituição para aplicar os limites de integração. Para voltarmos para a variável , vamos usar o triangulo:
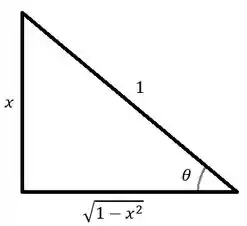
Então temos que, pela substituição
e pelo triangulo
logo
Voltando a nossa primeira integral do volume:
Aplicando os limites:
Resolvendo as operações de frações dentro dos parênteses:
Como o arco seno é uma função impar simétrica, , logo
Como
Prontinho! Tá aí o volume do nosso sólido.