Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.3 - Ex. 14

Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica.

x + y = 3 ,     x = 4 - ( y - 1 ) ²

Passo 1

Fala aí, pessoal! 😎

Nesse problema temos que obter o volume formado pela rotação da area entre as curvas x + y = 3 e x = 4 - ( y - 1 ) ² ao redor do eixo x .

Pra isso foi pedido que aplicássemos o método das cascas cilíndricas...

Tem ideia de como fazemos isso? 👀

Basicamente o método das cascas cilíndricas consiste em aplicar a formulinha

V = ∫ a b 2 π y x 1 - x 2 d y

Onde x 1 e x 2 são as equações que limitam nossa área.

Veja só! 😉

Passo 2

Nós temos os seguintes esboços, da região e casca típica:

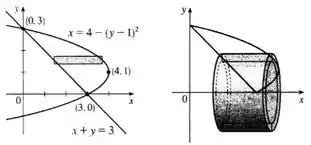
Como podemos ver no desenho, nossa função varia de 0 a 3 em y , então:

V = ∫ 0 3 2 π y 4 - y - 1 2 - 3 - y d y = 2 π ∫ 0 3 y - y 2 + 3 y d y

V = 2 π ∫ 0 3 - y 3 + 3 y 2 d y

Integrando pelo método de integração polinomial, temos

V = 2 π - 1 4 y 4 + y 3 0 3 = 2 π - 81 4 + 27

V = 2 π 27 4

V = 27 π 2

E aí! Legal, né? Responde Aí! 😉

Resposta

V = 27 π 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =2 y - y 2 ; x = 0
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: y = x ; y = 1