Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.Exercícios Práticos - Ex. 24
Use o método de Euler para resolver o problema de valor inicial no intervalo dado, começando em com .
Passo 1
Para encontrar os valores aproximados, usamos o método de Euler, fazendo:
E como temos que ir do ao , serão 20 etapas.
Esse problema pede para usar algum aplicativo ou calculadora para calcular os valores aproximados, então vamos montar uma tabela.
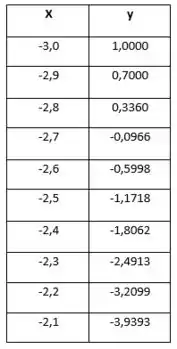
Prontinho😊
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Utilize o método de Euler para calcular as três primeiras aproximações do problema de valor inicial dado para o tamanho do incremento especificado. Calcule a solução exata e estude a precisão de suas
Utilize o método de Euler para calcular as três primeiras aproximações do problema de valor inicial dado para o tamanho do incremento especificado. Calcule a solução exata e estude a precisão de suas
26. Mostre que a aproximação b e 0 ( h )
1. O método de Euler modificado é deduzido a partir da figura abaixo: y ( x ) : solução exata da equação diferencial L 1 : z 1 ( x ) ; reta que passa por ( y n , x n ) e é tangente a y ( x ) em ( x n
18. Determine y ( 1 ) para y ' ' - 3 y ' + 2 y = 0 , y 0 = - 1 , y ' 0 = 0 utilizando o método de Euler com h = 0.1