Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 26
26. Mostre que a aproximação e
Passo 1
E aí meus queridos(as)!
Se liga só! A aproximação é dada pela seguinte fórmula abaixo...
E para essa aproximação, temos o seguinte gráfico...
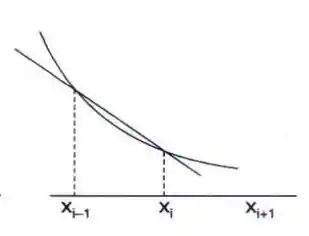
Passo 2
Com efeito, pela série de Taylor, temos que...
Em que é um ponto entre e
Passo 3
Dessa forma, o erro local é dado por:
Em que é tal que para todo . Logo, o erro local vai ser dado por .
Resposta
Exercícios de Livros Relacionados
Use o método de Euler com d x = 0,05 para estimar y(c), onde y é a solução para o problema de valor inicial dado. c = 4 ;d y d x =x 2 - 2 y + 1 x ,y 1 = 1
Use o método de Euler com d x = 0,05 para estimar y(c), onde y é a solução para o problema de valor inicial dado. c = 3 ;d y d x =x - 2 y x + 1 ,y 0 = 1
Use o método de Euler para resolver o problema de valor inicial no intervalo dado, começando em x 0 com d x = 0,1 . y ' = 2 - y 2 x + 3 , y - 3 = 1 ; - 3 ≤ x ≤ - 1 ;x 0 = - 3
Use o método de Euler para resolver o problema de valor inicial no intervalo dado, começando em x 0 com d x = 0,1 . y ' = y + cos x, y 0 = 0 ;0 ≤ x ≤ 2 ;x 0 = 0
Use o método de Euler com o passo especificado para calcular o valor da solução no ponto dado x*. Determine o valor da solução exata em x* y ' = 1 + y ² , y0 ,y 0 = 0 ² d x = 0,1 x * = 1