Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.2 - Ex. 29
Use o método do Exemplo 3 para ajudar a efetuar a derivação indicada:
Passo 1
Analisando a função a ser derivada, observamos se tratar de uma função complexa inserida dentro de uma função logarítmica. Nesse caso, as propriedade de logaritmo devem ser usadas antes de diferenciar a função envolvendo logaritmo.
Observe a estrutura da função a ser diferenciada:
Como a função está expressa em termos de logaritmo, usaremos as propriedades de logaritmo ao nosso favor. E aqui vamos usar duas propriedades de logaritmo importantes:
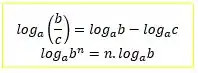
Aplicando essas propriedades na função:
O resultado dessa derivada é a subtração das derivadas dos logaritmos naturais:
Calcularemos essas derivadas separadamente, chamando as subfunções de e :
Passo 2
Primeiro, vamos resolver a derivada :
Usaremos a Regra da Cadeia, onde:
E os termos e resolvendo as derivadas:
Aplicando na Regra da Cadeia :
Reorganizando a fórmula, temos:
Passo 3
Agora, vamos resolver a derivada :
Usaremos a Regra da Cadeia, onde:
E os termos e resolvendo as derivadas:
Aplicando na Regra da Cadeia :
Simplificando temos:
Passo 4
Retornando para o foco principal do problema, a resolução da diferenciação logarítmica :