Use o método de Newton para encontrar o valor máximo absoluto da função , com precisão de seis casas decimais.

Para achar a derivada de vamos usar algumas regras de derivação, a do produto, da função trigonométrica e do polinômio:

Vamos calcular e :

Aqui a gente aplica a regra do produto:

E para segunda derivada, temos:

Vamos precisar aplicar a regra do produto no segundo termo:

Agora vamos aplicar no método!!

Pronto, agora que temos e é só jogar na fórmula de Newton:

Vamos agora analisar qual valor usar para , a gente costuma fazer isso, em casos que a questão não nos da um a gente precisa analisar o gráfico a função, pois a partir dele a gente consegue uma boa estimativa de onde está localizda nossa raiz.

Um outra forma de se avaliar um bom local é analisar a função, em situações que a função permite isso, podemos avaliar onde um possível valor tornaria aquela função .

Iremos plotar o nosso gráfico utilizando o Desmos.

Pelo gráfico abaixo de , parece ter ponto de intersecção em , veja:

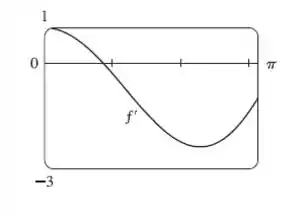
Agora vamos substituir no método:

Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:

Mais uma vez, agora com :

Pronto, o valor não varia mais, então a raiz é .

Vamos checar o intervalo, para ver mesmo se é o máximo absoluto, precisamos observar os valores nos extremos do intervalo:

Como desses o nosso valor é o maior, temos então o nosso ponto máximo do intervalo.

Entendeu direitinho?? Responde aeee!! 😉