Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 69
Use multiplicação ou divisão de séries de potências para encontrar os três primeiros termos diferentes de zero na série de Maclaurin de cada função.
Passo 1
Faaaala galerinha! Tudo na paz com vocês? Espero que sim! Partiu!?
Analisando a questão, percebemos que ela solicita que encontramos os três primeiros termos diferente de zero da série de Maclaurin para a função utilizando de multiplicação ou divisão de séries de potências.
Mas como eu resolvo isso ai?
Bom, vamos analisar a Tabela 1 e verificar se encontramos alguma série que se parece com a função .
Observe que temos uma série para e não temos uma série para .
Já o termo , precisamos fazer a derivada. A função vai ficar com a cara de um somatório bem conhecido, a série geométrica.
Feito isso, integramos e logo obtemos a série de . Ai por fim é só nos multiplicarmos as duas séries.
Com esse bizu, ficou mumu fazer essa ein!? Vamos juntos gabaritar!
Passo 2
Já conhecemos a série de , então vamos calcular a de .
Primeiro vamos derivar:
Agora compare bem com a série geométrica:
Só colocarmos o sinal de menos em evidência, logo
Então, integrando dos dois lados
Como é uma integral indefinida, vai aparecer uma constante .
Para calcular a constante, vamos substituir , pois sabendo que neste ponto a série zera:
Logo, temos que
Como sabemos que:
Fazendo a multiplicação das séries:
Vamos ter:
Passo 3
Agora vamos fazer a multiplicação com os três primeiros termos, porque o enunciado solicitou isso.
Para facilitar, vamos utilizar o método do chuveirinho
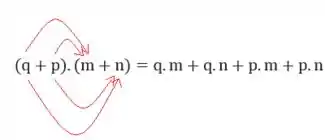
Vamos começar:
Como vai ser uma conta muito grande, vamos dividir em quatro partes, depois somamos tudo
Parte :
Parte :
Parte :
Parte :
Agora vamos somar tudo, e não podemos esquecer do sinal de menos que tinha na frente da multiplicação:
Logo, os três primeiros termos do somatório da função é: