Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.6 - Ex. 76
Use qualquer método para encontrar a área da região delimitada pelas curvas.
Passo 1
Para calcular a região entre curvas precisamos montar a integral:
E achar o valor dela. Vamos lá!
Passo 2
Vamos olhar nossa região em um gráfico:
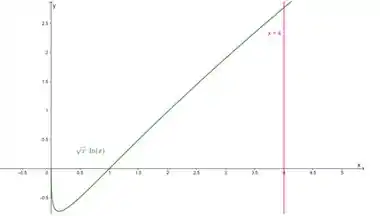
Vemos que a função maior é , a menor é , e temos os extremos de integração:
E o outro extremo é a interseção entre é e , dá até para ver no gráfico. Saca só:
Nossa integral fica então com essa carinha:
Passo 3
Agora é só calcular. Podemos tentar usar a Fórmula 50 da tabela de integrais:
Reescrevendo nossa integral:
Fazendo :
Fazendo essas continhas, temos que:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Use as identidades cos 2 θ = 1 - 2 sin 2 θ = 2 cos 2 θ - 1 para ajudar a calcular as integrais: a ∫ s i n 2 x 2d x a ∫ c o s 2 x 2d x
A velociadade do som no ar a 0 ° C ( 273K , na escala Kelvin) é 1.087 pés por segundo, mas a velocidade v aumenta à medida que a temperatura T sobe. Experimentos mostraram que a taxa de variação de v
Lembre que d d x arcsec x = 1 x x 2 - 1 Use isso para conferir a Fórmula 14 na Tabela 5.2 . 1 .
Sejam F e G as funções definidas por: F x = x 2 + 3 x x e G x = x + 3 x0 x ,x0 ( a ) Mostre que F e G têm a mesma derivada. ( b ) Mostre que G x ≠ F x + C com qualquer constante C . ( c ) As partes (
( a ) Mostre que F x = arctan x e G x = - arctan 1 x diferem por uma constante no intervalo ( 0 ,+ ∞ ) mostrando que ambas as funções são antiderivadas de uma mesma função. ( b ) Encontre a consta