(a) Use um recurso computacional para obter o gráfico da função .
(b) Use o gráfico de (a) para fazer um esboço do gráfico de .
(c) Encontre e verifique seu trabalho em (b) usando o recurso computacional para obter o gráfico de .
(d) Encontre a equação da reta tangente ao gráfico de em e faça o gráfico de junto com o da reta tangente
Passo 1
Falaaa aí! Tudo joia?
Vamos usar nosso amiguinho Geogebra aqui pra fazer os gráficos, beleza?
Pra começar, o gráfico de :
-
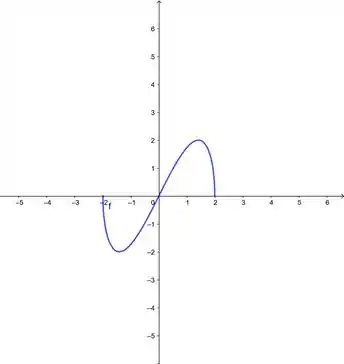
Passo 2
- Agora a gente vai fazer . O próprio Geogebra faz, quer ver?
- Agora vamos calcular a derivada de direitinho...
- Agora vamos usar a derivada que a gente calculou pra encontrar a equação da reta tangente. Lembrando que ela tem essa forma aqui:
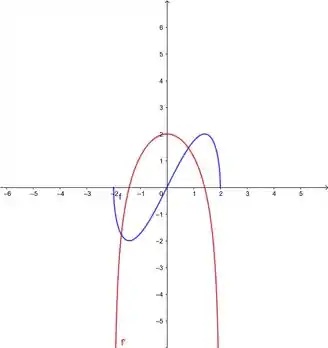
Passo 3
Usando regra do Produto e Regra da Cadeia, hein, não esquece!
Show! Essa é a derivada! Vamos plotar o gráfico dela junto com o nosso gráfico agora:
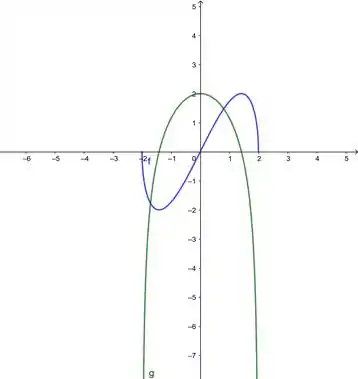
Deu igualzinha a de cima, viu? Nossa derivada tá certinha então! 😉
Passo 4
No nosso caso, , então a gente tem:
Nossa reta tangente então é:
Essa é a reta tangente! Vamos plotar ela lá no gráfico agora:
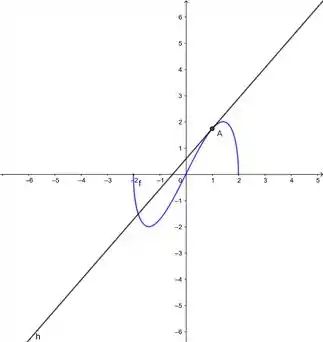
E finalizamos por aqui! 😊
Resposta
- Gráfico.
- Gráfico.