Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 32

Use um recurso gráfico computacional para estimar os valores máximo e mínimo absolutos de f , se houver, nos intervalos indicados e use os métodos do Cálculo para obter os valores exatos.

f x = x x 2 + 2 ; [ - 1,4 ]

Passo 1

Oii tudo bem?

Mais uma de máximo e mínimo aí pra a gente!

Primeiro vamos ver usando um gráfico da função. Eu plotei no Geogebra e deu isso aqui oh:

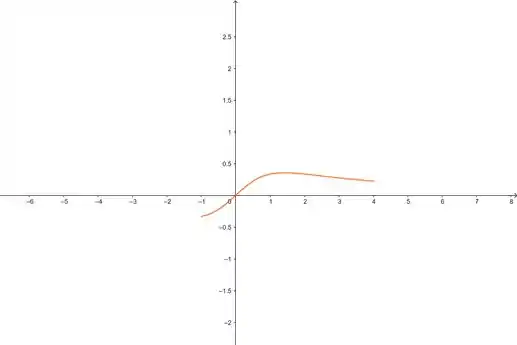
Pelo gráfico aqui, a gente vê que tem um ponto mínimo em x = - 1 e um máximo ali em x = 1 aproximadamente. Vamos calcular o valor exato agora...

Passo 2

Vamos derivar a função...

f ' x = 1 x 2 + 2 - 2 x x x 2 + 2 2 = - x 2 + 2 x 2 + 2 2

Isso vai zerar quando a função de cima zerar...

- x 2 + 2 = 0

x 2 = 2

x =   ± 2

x ≅ ± 1,41

No caso o que está dentro do nosso intervalo é só o 1,41 .

Passo 3

Vamos testar o valor da função nesse ponto e nos pontos do intervalo agora:

f - 1 =   - 1 - 1 2 + 2 =   - 1 3  

f 2 = 2 2 + 2 = 2 4 ≅ 0,35

f 4 = 4 16 + 2 = 4 18 = 2 9 ≅ 0,22

Então temos um ponto máximo em x = 2 e um mínimo em x = - 1 . Mais ou menos o que a gente previu mesmo né? Prontinho! 😉

Resposta

Pontos de mínimo absoluto em x = - 1

Ponto de máximo: x = 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize e identifique os valores extremos absolutos de: a) l n ⁡ ( cos ⁡ x )e mπ 4 , π 3 b) cos ⁡ ( ln ⁡ x )e m1 2 , 2
Determine os valores das constantes a, b, c e d de modo que f x = a x 3 + b x 2 + c x + d tenha um máximo local no ponto (0,0) e um mínimo local no ponto (1,-1).
Determine os valores máximo e mínimo absolutos de f x = e x - 2 x em [ 0,1 ] .
Discuta o comportamento de valor extremo da função f x = xs e n 1 x ,x ≠ 0 . Quantos pontos críticos ela possui? Onde estão localizados no eixo x? f tem um mínimo absoluto? Um máximo absoluto?
Determine os valores das constantes a e b de modo que f x = a x 2 + b x tenha um máximo absoluto no ponto (1, 2).