Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.4 - Ex. 26
Use um recurso gráfico para estimar o valor de usando um zoom no gráfico de e, então, compare sua estimativa ao valor exato obtido por derivação.
Passo 1
Cara, então vamos ao recurso gráfico né? O gráfico desse cara é:
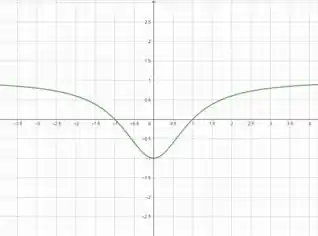
E como vamos estimar a derivada dessa função no ponto ?
Cara, a derivada de uma função em um ponto é justamente o coeficiente angular da reta tangente a essa função nesse ponto. E o coeficiente angular dessa reta é a tangente do ângulo que ela faz com o eixo . Show?
Passo 2
Então, vamos traçar essa reta tangente à função no ponto :
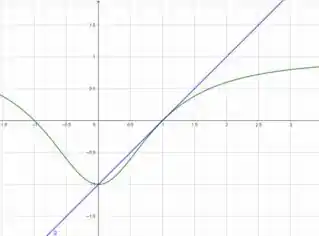
Como queremos uma estimativa, não precisamos fazer nada perfeito, ok? Então, só coloquei uma reta que passasse no ponto , que é o ponto que queremos da função, que é essa reta em azul.
Agora, olhando bem para ela, qual seria a tangente do seu ângulo com o eixo ? Bom, para calcular a tangente podemos usar esse triângulo em azul que aparece aqui:
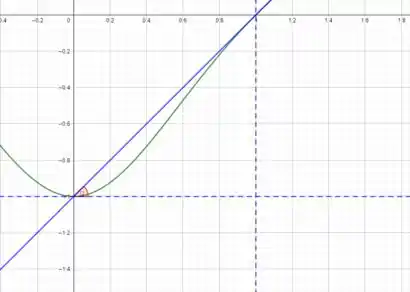
E agora podemos achar o valor da tangente daquele ali, dividindo o cateto oposto pelo adjacente. Pelo gráfico, vemos que o cateto oposto tem tamanho e o adjacente também:
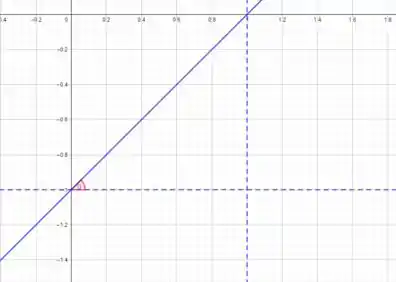
Dessa forma, .
Como a derivada é o valor da tangente desse ângulo, pelas nossas estimativas, ela será 1, também!!
Passo 3
Agora, vamos conferir se isso está certo, usando derivação de fato:
Temos:
E sua derivada será calculada pela regra do quociente:
Passo 4
Agora, falta só achar o valor dessa derivada no ponto :
Temos:
Substituindo por :
Opa, casou com a nossa estimativa hein hehe. Tudo certo, então, a derivada da função no ponto é mesmo igual a .