Use um recurso gráfico para obter uma estimativa da localização das linhas tangentes horizontais. Depois, encontre a localização exata por diferenciação.
Passo 1
Utilizando, primeiro, o recurso gráfico que o problema fala, temos essa imagem aqui:
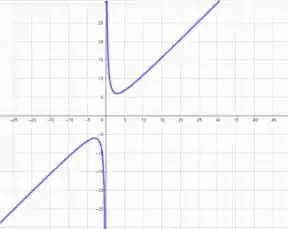
Bom, essa estimativa que ele pede vai ser no olho mesmo, ok? E, no olho, a gente pode ver que a linha tangente ao gráfico horizontal deve aparecer ali mais ou menos nos pontos e .
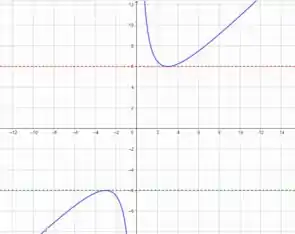
Para achar os pares coordenados, é só substituir o valor do na função e, com isso, a gente acharia os pares: e , respectivamente.
Passo 2
Masss, infelizmente, nem tudo são flores né? Rs
E agora vamos para a segunda parte do problema, onde vamos achar as localizações exatas dos pontos em que a reta tangente é horizontal, usando a diferenciação.
Vamos, então, lembrar rapidinho da teoria: uma reta tangente a uma função em um ponto deve ter o mesmo valor que a função nesse ponto e sua inclinação é a derivada da função nesse ponto. Essa reta tangente é horizontal quando sua inclinação é zero, certo? Logo, a derivada da função no ponto em questão também deve ser zero! Ou seja, para achar as localizações exatas dos pontos em que a reta tangente é horizontal, só precisamos achar onde que a derivada da função é zero!
Passo 3
Então, temos a função:
Que pode ser escrita assim:
Vamos derivar e igualar o resultado a zero:
Bom, nós temos que resolver essa coisa aí agora.
Passo 4
Temos:
Arrumando esse cara:
Então, esses são os pontos em que a reta tangente é horizontal, ou seja, em que a derivada da função é zero!
Ora ora, e não é que nosso olho funcionou direitinho? Os pontos realmente eram e . Logo, já até sabemos as respostas, são os mesmos pares ordenados que já vimos ali em cima: e .
OBS.: Cara, dessa vez, o nosso olho deu certo (amém?), mas normalmente isso não é um método muito confiável de se usar hein. A melhor forma é usando diferenciação mesmo! Porque não tem erro! Beleza?
Resposta
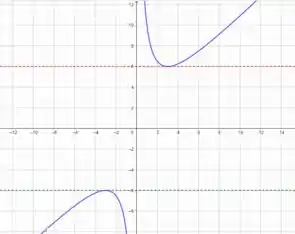
Retas tangentes horizontais em e .